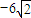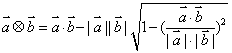题目内容
若规定向量的运算符号“?”的运算规则为:
?
=
•
-|
||
|
(其中
•
表示向量
与
的数量积),若|
|=2,|
|=3,则
?
的最小值为( )
| a |
| b |
| a |
| b |
| a |
| b |
1-(
|
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
分析:由题意可得
•
=6cosθ,故
?
=6cosθ-2×3
=6
sin(
-θ ),由 (
-θ ) 的
范围可得当(
-θ )=-
时,
?
有最小值等于-6
.
| a |
| b |
| a |
| b |
| 1-cos2θ |
| 2 |
| π |
| 4 |
| π |
| 4 |
范围可得当(
| π |
| 4 |
| π |
| 2 |
| a |
| b |
| 2 |
解答:解:设
与
的夹角为θ,由题意可得
•
=2×3cosθ=6cosθ.
∴
?
=6cosθ-2×3
=6cosθ-6sinθ=6
sin(
-θ ).
由于0≤θ≤π,∴-
≤(
-θ )≤
,故当 (
-θ )=-
时,
?
有最小值等于-6
,故选A.
| a |
| b |
| a |
| b |
∴
| a |
| b |
| 1-cos2θ |
| 2 |
| π |
| 4 |
由于0≤θ≤π,∴-
| 3π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
| a |
| b |
| 2 |
点评:本题考查两个向量的数量积的定义,正弦函数的定义域和值域,是一道中档题.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案
相关题目
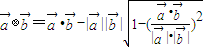 ,若
,若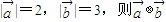 的最小值为( )
的最小值为( )