题目内容
已知圆C：（x-3）2+（y+1）2=2，则在坐标轴上的截距相等且与圆相切的直线有 ________条．
3
分析：先看直线不过原点的情况，设出直线的方程，斜率为-1，则可知这样的直线有2条，再看直线过原点的情况，把原点代入即可知原点在圆外，则这样的直线也应该有2条，最后验证以上4条中有一条是重复，最后综合得到结论．
解答：若直线不过原点
则
+
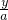=1
斜率=-1
则应该有2条
若过原点
把（0，0）代入（0-3）2+（y+1）2＞2
即原点在圆外
所以过原点有2条切线
下面检验过原点且斜率等于-1的
是x+y=0
圆心（3，-1）到x+y=0距离=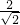
=
=半径
所以x+y=0是切线
即上面4条有重复的
所以一共有3条
点评：本题主要考查了直线与圆的位置关系．考查了学生数形结合的思想和对基本知识的理解．
分析：先看直线不过原点的情况，设出直线的方程，斜率为-1，则可知这样的直线有2条，再看直线过原点的情况，把原点代入即可知原点在圆外，则这样的直线也应该有2条，最后验证以上4条中有一条是重复，最后综合得到结论．
解答：若直线不过原点
则
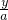+=1斜率=-1
则应该有2条
若过原点
把（0，0）代入（0-3）2+（y+1）2＞2
即原点在圆外
所以过原点有2条切线
下面检验过原点且斜率等于-1的
是x+y=0
圆心（3，-1）到x+y=0距离=
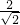==半径所以x+y=0是切线
即上面4条有重复的
所以一共有3条
点评：本题主要考查了直线与圆的位置关系．考查了学生数形结合的思想和对基本知识的理解．
练习册系列答案
夺冠金卷全能练考系列答案
相关题目
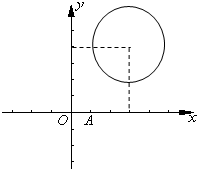已知圆C：（x-3）2+（y-4）2=4，