题目内容
将函数y=sinx按向量
=（-
，3）平移后的函数解析式为（ ）
| a |
| π |
| 4 |
A、y=sin（x-
| ||
B、y=sin（x-
| ||
C、y=sin（x+
| ||
D、y=sin（x+
|
分析：直接利用函数的图象的平移公式，求出平移后的函数的解析式即可．
解答：解：由
得
∴y′-3=sin（x'+
）．
∴y′=sin（x'+
）+3，
即y=sin（x+
）+3．
故选C
|
|
∴y′-3=sin（x'+
| π |
| 4 |
∴y′=sin（x'+
| π |
| 4 |
即y=sin（x+
| π |
| 4 |
故选C
点评：本题是基础题，考查三角函数的图象的平移，注意向量的平移的应用，平移公式中坐标的区别．
练习册系列答案
相关题目
=(－
，3)平移后的函数的解析式为
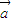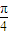,3)平移后的函数解析式为( )
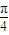)+3 B.y=sin(x-
)-3
)+3 D.y=sin(x+
)-3
=（-
，3）平移后的函数解析式为（ ）
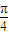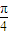）+3
）-3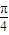
）+3
）-3