Question

已知函数f（x）=cosωx（ω＞0），x∈R．
（1）当ω=2时，求函数f（x）取得最大值时x的集合；
（2）若函数f（x）的图象过点，且在区间上是单调函数，求ω的值；
（3）在（2）的条件下，若，画出函数y=f（x）在上的图象．

Answer 1

解：（1）当ω=2时，函数f（x）=cos2x． 当函数f（x）=cos2x取得最大值时，2x=2kπ，k∈Z，即x=kπ，k∈Z．（2分）
∴当ω=2时，函数f（x）取得最大值时x的集合为{x|x=kπ，k∈Z}．（3分）
（2）∵f（x）的图象过点，
∴．（4分）
又ω＞0，
∴，k∈N，∴．（5分）
当k=0时，，在区间上是减函数； （6分）
当k=1时，ω=2，f（x）=cos2x在区间上是减函数； （7分）
当k≥2时，，f（x）=cosωx在区间上不是单调函数．（8分）
综上，或ω=2．（9分）
（3）由（2）知满足的函数为f（x）=cos2x，列表：

2x	-	0		π
x		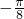0
cos2x		1	0	-1

（10分）
其在区间上的图象是：
（12分）
分析：（1）当ω=2时，函数f（x）=cos2x，当函数f（x）=cos2x取得最大值时，由2x=2kπ，k∈Z，求出x的集合．
（2）由f（x）的图象过点，可得，又ω＞0，可得 ；经过检验，当k=0或1 时，满足条件，从而得到ω的值．
当k≥2时，不满足条件．
（3）由（2）知满足的函数为f（x）=cos2x，列表，在坐标系中描点作图．
点评：本题主要考查利用y=Asin（ωx+∅）的图象特征，余弦函数的单调性和最值的求法，属于中档题．