题目内容
已知函数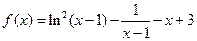 .
.
(Ⅰ)求函数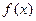 的单调区间;
的单调区间;
(Ⅱ)若当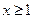 时,不等式
时,不等式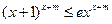 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
解:(Ⅰ)函数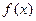 的定义域为
的定义域为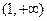 ………………………………………1分
………………………………………1分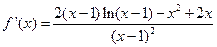 ……………………………………………3分
……………………………………………3分
令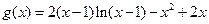
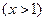 且
且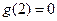 …………………4分
…………………4分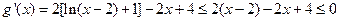
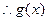 在
在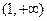 为单调递减函数,
为单调递减函数,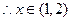 时,
时,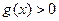
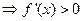 ;
;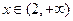 时,
时,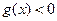
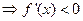 ;
;
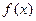 递增区间为
递增区间为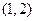 ;递减区间为
;递减区间为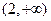 。………………………………6分
。………………………………6分
(Ⅱ)在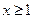 条件下:
条件下: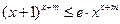 恒成立
恒成立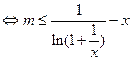 恒成立。 ………………………………8分
恒成立。 ………………………………8分
令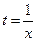 ,设
,设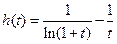 (
(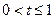 )
)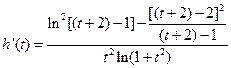 ……………………………10分
……………………………10分
由(Ⅰ)知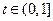 时,
时,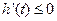 ,
,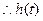 在
在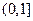 单调递减
单调递减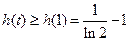 ,即
,即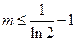
 的取值范围为
的取值范围为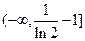 ………………………………………12分
………………………………………12分
解析

练习册系列答案
相关题目
已知函数 .
.
(1)求 的最小值;
的最小值;
(2)当函数自变量的取值区间与对应函数值的取值区间相同时,这样的区间称为函数的保值区间.设 ,试问函数
,试问函数 在
在 上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.
上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.
已知函数 的定义域为
的定义域为 ,若
,若 在
在 上为增函数,则称
上为增函数,则称 为“一阶比增函数”;若
为“一阶比增函数”;若 在
在 上为增函数,则称
上为增函数,则称 为“二阶比增函数”.我们把所有“一阶比增函数”组成的集合记为
为“二阶比增函数”.我们把所有“一阶比增函数”组成的集合记为 ,所有“二阶比增函数”组成的集合记为
,所有“二阶比增函数”组成的集合记为 .
.
(Ⅰ)已知函数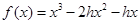 ,若
,若 且
且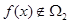 ,求实数
,求实数 的取值范围;
的取值范围;
(Ⅱ)已知 ,
, 且
且 的部分函数值由下表给出,
的部分函数值由下表给出,
|
|
|
|
|
|
|
|
|
|
|
|
求证: ;
;
(Ⅲ)定义集合
请问:是否存在常数 ,使得
,使得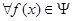 ,
, ,有
,有 成立?若存在,求出
成立?若存在,求出 的最小值;若不存在,说明理由.
的最小值;若不存在,说明理由.


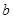
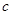




 ,编写一个程序求函数值.
,编写一个程序求函数值. 试画出求函数值的程序框图.
试画出求函数值的程序框图.