题目内容
已知数列 的前n项和为
的前n项和为 ,且
,且
 ,
,
(1)求数列 的通项公式;
的通项公式;
(2) 令 ,且数列
,且数列 的前n项和为
的前n项和为 ,求
,求 ;
;
(3)若数列 满足条件:
满足条件: ,又
,又 ,是否存在实数
,是否存在实数 ,使得数列
,使得数列 为等差数列?
为等差数列?
 的前n项和为
的前n项和为 ,且
,且
 ,
,(1)求数列
 的通项公式;
的通项公式;(2) 令
 ,且数列
,且数列 的前n项和为
的前n项和为 ,求
,求 ;
;(3)若数列
 满足条件:
满足条件: ,又
,又 ,是否存在实数
,是否存在实数 ,使得数列
,使得数列 为等差数列?
为等差数列?(1)
(2)


(3)

(2)



(3)

本试题主要考查了数列中通项公式的求解,数列的求和,以及判定数列是否为等差数列的概念的综合运用。
(1)利用数列 的前n项和为
的前n项和为 ,且
,且
 ,,对n讨论,得到关于通项公式和前n项和的关系式,进而得到通项公式。
,,对n讨论,得到关于通项公式和前n项和的关系式,进而得到通项公式。
(2)利用裂项求和的思想,找到通项公式的特点,再累加得到
(3)假设存在这样的实数,满足条件,
然后根据假设得到 ,分析其值,得到存在
,分析其值,得到存在
(1)n=1时,
n

(2) ,
,



(3) ,即
,即 ,
,
假设存在这样的实数,满足条件,
又 ,
, ,
, ,
,

即:
解得: ,此时:
,此时:
 ,
,
数列 是一个等差数列。
是一个等差数列。
所以
(1)利用数列
 的前n项和为
的前n项和为 ,且
,且
 ,,对n讨论,得到关于通项公式和前n项和的关系式,进而得到通项公式。
,,对n讨论,得到关于通项公式和前n项和的关系式,进而得到通项公式。(2)利用裂项求和的思想,找到通项公式的特点,再累加得到
(3)假设存在这样的实数,满足条件,
然后根据假设得到
 ,分析其值,得到存在
,分析其值,得到存在
(1)n=1时,

n


(2)
 ,
,


(3)
 ,即
,即 ,
,假设存在这样的实数,满足条件,
又
 ,
, ,
, ,
,
即:

解得:
 ,此时:
,此时: ,
,数列
 是一个等差数列。
是一个等差数列。所以


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
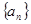 中,
中,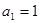 ,
,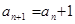 ,则
,则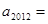
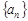 中,
中,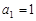 ,
,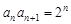
 ,则数列
,则数列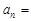 .
. 的通项公式为
的通项公式为 , 则它的公差为 ( )
, 则它的公差为 ( )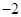
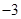
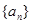 的公差
的公差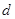 大于0,且
大于0,且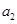 、
、 是方程
是方程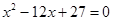 的两根.数列
的两根.数列 的前
的前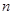 项和为
项和为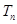 ,满足
,满足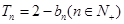
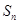 ,记
,记 .若
.若 为数列
为数列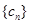 中的最大项,求实数
中的最大项,求实数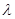 的取值范围.
的取值范围. }中,
}中, =1,前n项和
=1,前n项和 。
。
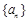 中,已知
中,已知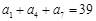 ,
,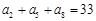 ,则
,则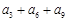 的值是( )
的值是( ) 为等差数列,且
为等差数列,且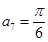 ,则
,则 .
.