Question

已知α为第二象限的角，sinα=,β为第一象限的角，cosβ=，求tan(2α-β)的值.

Answer 1

解法一：∵tan(2α-β)=,α为第二象限角，sinα=,

∴cosα=,

tanα=.

∴tan2α=.

∵β为第一象限角，cosβ=

∴sinβ=,tanβ=.

∴tan(2α-β)=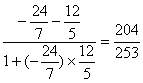

解法二：∵α为第二象限角，sinα=,

∴cosα=.

∵β为第一象限角，cosβ=,

∴sinβ=.

故sin2α=2sinαcosα=,

cos2α=1-2sin²α=.

sin(2α-β)=sin2αcosβ-cos2αsinβ=-,

cos(2α-β)=cos2αcosβ+sin2αsinβ=,

∴tan(2α-β)=.