题目内容
若x-1，x，x+1是钝角三角形的三边长，则实数x的取值范围
（2，4）
（2，4）
．分析：判断出x+1为最大边，设x+1对应的角为α，利用余弦定理表示出cosα，得到cosα小于0，求出不等式的解集即可确定出x的范围．
解答：解：∵x-1，x，x+1是钝角三角形的三边长，且x+1为最大边，对应的角设为α，
∴cosα=
＜0，
整理得：
=
＜0，即（x-4）（x-1）＜0，
解得：1＜x＜4，
∵x-1+x＞x+1，即x＞2，
则实数x的取值范围为（2，4）．
故答案为：（2，4）
∴cosα=
| (x-1)2+x2-(x+1)2 |
| 2x(x-1) |
整理得：
| x(x-4) |
| 2x(x-1) |
| x-4 |
| 2(x-1) |
解得：1＜x＜4，
∵x-1+x＞x+1，即x＞2，
则实数x的取值范围为（2，4）．
故答案为：（2，4）
点评：此题考查了余弦定理，其他不等式的解法，以及三角形的三边关系，熟练掌握余弦定理是解本题的关键．
练习册系列答案
相关题目
若函数f（x）（x∈R）为奇函数，且存在反函数f-1（x）（与f（x）不同），F(x)=
，则下列关于函数F（x）的奇偶性的说法中正确的是（ ）
| 2f(x)-2f-1(x) |
| 2f(x)+2f-1(x) |
| A、F（x）是奇函数非偶函数 |
| B、F（x）是偶函数非奇函数 |
| C、F（x）既是奇函数又是偶函数 |
| D、F（x）既非奇函数又非偶函数 |
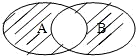如图所示的韦恩图中，A，B是非空集合，定义集合A#B为阴影部分表示的集合．若x，y∈R，A={x|y=
}，B={y|y=3x，x＞0}，则A#B=