题目内容
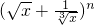 展开式的各项系数和大于8且小于32,则展开式中系数最大的项是
展开式的各项系数和大于8且小于32,则展开式中系数最大的项是
- A.
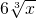
- B.
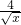
- C.
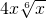
- D.
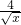 或
或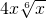
A
分析:通过已知条件,求出二项式各项系数和,利用系数和大于8且小于32,解出n的值,利用二项展开式系数的性质,即可求出展开式中系数最大的项.
解答:令x=1,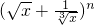 展开式的各项系数和为2n,因为
展开式的各项系数和为2n,因为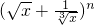 展开式的各项系数和大于8且小于32,
展开式的各项系数和大于8且小于32,
所以8<2n<32,所以n=4,展开式中间项的系数最大,
即第3项二项式系数最大, =
=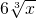 .
.
故选A.
点评:本题是基础题,考查二项式系数的性质,考查计算能力,常考题型.
分析:通过已知条件,求出二项式各项系数和,利用系数和大于8且小于32,解出n的值,利用二项展开式系数的性质,即可求出展开式中系数最大的项.
解答:令x=1,
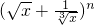 展开式的各项系数和为2n,因为
展开式的各项系数和为2n,因为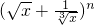 展开式的各项系数和大于8且小于32,
展开式的各项系数和大于8且小于32,所以8<2n<32,所以n=4,展开式中间项的系数最大,
即第3项二项式系数最大,
 =
=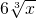 .
.故选A.
点评:本题是基础题,考查二项式系数的性质,考查计算能力,常考题型.

练习册系列答案
 目标测试系列答案
目标测试系列答案
相关题目
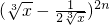 展开式中偶数项二项式系数的和比(1+x)n展开式的各项系数和大112.
展开式中偶数项二项式系数的和比(1+x)n展开式的各项系数和大112.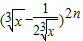 展开式中偶数项二项式系数的和比(1+x)n展开式的各项系数和大112.
展开式中偶数项二项式系数的和比(1+x)n展开式的各项系数和大112.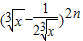 展开式中的所有的有理项.
展开式中的所有的有理项.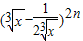 展开式中偶数项二项式系数的和比(1+x)n展开式的各项系数和大112.
展开式中偶数项二项式系数的和比(1+x)n展开式的各项系数和大112.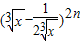 展开式中的所有的有理项.
展开式中的所有的有理项.