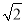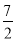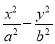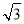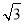题目内容
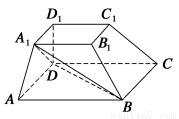
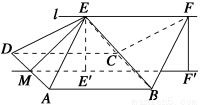
如图,四边形ABCD是边长为2的正方形,直线l与平面ABCD平行,E和F是l上的两个不同点,且EA=ED,FB=FC.E′和F′是平面ABCD内的两点,EE′和FF′都与平面ABCD垂直.

(1)证明:直线E′F′垂直且平分线段AD;
(2)若∠EAD=∠EAB=60 °,EF=2.求多面体ABCDEF的体积.
(1)见解析(2)2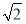 .
.
【解析】(1)证明 ∵EA=ED且EE′⊥平面ABCD,
∴E′D=E′A,∴点E′在线段AD的垂直平分线上.
同理,点F′在线段BC的垂直平分线上.
又四边形ABCD是正方形,
∴线段BC的垂直平分线也就是线段AD的垂直平分线,即点E′、F′都在线段AD的垂直平分线上.
∴直线E′F′垂直且平分线段AD.
(2)解 如图,连接EB、EC,由题意知多面体ABCDEF可分割成正四棱锥E?ABCD和正四面体E?BCF两部分.设AD的中点为M,在Rt△MEE′中,由于ME′=1,ME=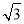 ,∴EE′=
,∴EE′=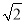 .
.
∴VE?ABCD=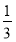 ·S正方形ABCD·EE′=
·S正方形ABCD·EE′=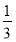 ×22×
×22×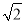 =
=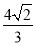 .
.
又VE?BCF=VC?BEF=VC?BEA=VE?ABC= S△ABC·EE′=
S△ABC·EE′=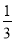 ×
×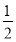 ×22×
×22×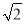 =
=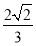 ,
,
∴多面体ABCDEF的体积为VE?ABCD+VE?BCF=2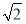 .
.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目