题目内容
已知函数f(x)=a·4x-2x+1+a+3。
(1)若a=0,解方程f(2x)=-5;
(2)若a=1,求f(x)的单调区间;
(3)若存在实数x0∈[-1,1],使f(x0)=4,求实数a的取值范围。
(1)若a=0,解方程f(2x)=-5;
(2)若a=1,求f(x)的单调区间;
(3)若存在实数x0∈[-1,1],使f(x0)=4,求实数a的取值范围。
解:(1)若a=0,由f(2x)=-5,即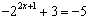 ,解得:x=1。
,解得:x=1。
(2)若a=1,则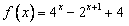 ,
,
设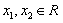 ,且
,且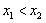 ,
,
则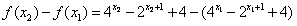
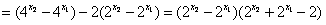 ,
,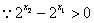
①当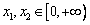 时,有
时,有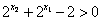 ,
,
∴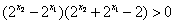 ,∴
,∴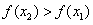 ,
,
∴f(x)在[0,+∞)上是增函数;
②当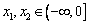 时,有
时,有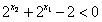 ,
,
∴ ,∴
,∴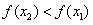 ,
,
∴f(x)在(-∞,0]上是减函数;
∴f(x)的单调增区间是[0,+∞),单调减区间是(-∞,0]。
(3)设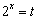 ,由
,由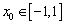 ,得
,得 ,
,
且 ,
,
∴存在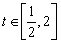 ,使得
,使得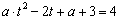 ,即
,即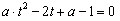 ,
,
令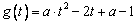 ,
,
若a≠0,则函数g(t)的对称轴是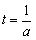 ,
,
由已知得:方程g(t)=0在 上有实数解,
上有实数解,
∴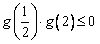 , ①
, ①
或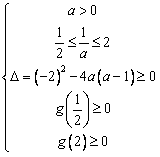 , ②
, ②
由不等式①得: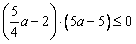 ,∴
,∴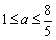 ,
,
由不等式组②得: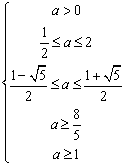 ,∴
,∴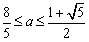 ,
,
所以,实数a的取值范围是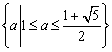 。
。

练习册系列答案
相关题目
已知函数f(x)=a-
,若f(x)为奇函数,则a=( )
| 1 |
| 2x+1 |
A、
| ||
| B、2 | ||
C、
| ||
| D、3 |