题目内容
已知圆M经过三点A(2,2),B(2,4),C(3,3),从圆M外一点P(a,b)向该圆引切线PT,T为切点,且|PT|=|PO|(O为坐标原点).
(1)求圆M的方程;
(2)试判断点P是否总在某一定直线上,若是,求出该直线方程;若不是,请说明理由.
(1)求圆M的方程;
(2)试判断点P是否总在某一定直线上,若是,求出该直线方程;若不是,请说明理由.
分析:(1)解法一:设圆M的方程为x2+y2+Dx+Ey+F=0,将三点A(2,2),B(2,4),C(3,3)代入可求;
解法二:设圆M的方程为(x-a)2+(y-b)2=r2(r>0),将三点A(2,2),B(2,4),C(3,3)代入可求;
解法三:求线段AB的垂直平分线与线段AC的垂直平分线的交点,可求圆心M的坐标,进而可求圆M的半径,从而可求圆M的方程;
解法四:可判断△ABC是直角三角形,进而可求圆M的圆心M的坐标为AB的中点(2,3),半径r=
|AB|=1,从而可求圆M的方程;
(2)连接PM,根据|PT|=
=
,|PO|=
,利用|PT|=|PO|,可判断点P总在定直线上.
解法二:设圆M的方程为(x-a)2+(y-b)2=r2(r>0),将三点A(2,2),B(2,4),C(3,3)代入可求;
解法三:求线段AB的垂直平分线与线段AC的垂直平分线的交点,可求圆心M的坐标,进而可求圆M的半径,从而可求圆M的方程;
解法四:可判断△ABC是直角三角形,进而可求圆M的圆心M的坐标为AB的中点(2,3),半径r=
| 1 |
| 2 |
(2)连接PM,根据|PT|=
| |PM|2-12 |
| (a-2)2+(b-3)2-1 |
| a2+b2 |
解答:解:(1)解法一:设圆M的方程为x2+y2+Dx+Ey+F=0,…(1分)
∵圆M经过三点A(2,2),B(2,4),C(3,3),
∴
…(4分)
解得
…(7分)
∴圆M的方程为(x-2)2+(y-3)2=1.…(8分)
解法二:设圆M的方程为(x-a)2+(y-b)2=r2(r>0),…(1分)
∵圆M经过三点A(2,2),B(2,4),C(3,3),
∴
…(4分)
解得
…(7分)
∴圆M的方程为(x-2)2+(y-3)2=1.…(8分)
解法三:∵A(2,2),B(2,4),
∴线段AB的垂直平分线方程为y=3,…(2分)
∵A(2,2),C(3,3),
∴线段AC的垂直平分线方程为y-
=-(x-
)即x+y-5=0,…(4分)
由
解得圆心M的坐标为(2,3).…(6分)
故圆M的半径r=|AM|=
=1.
∴圆M的方程为(x-2)2+(y-3)2=1.…(8分)
解法四:∵|AB|=
=2,|AC|=
=
,|BC|=
=
,…(2分)
∴|AC|2+|BC|2=4=|AB|2.
∴△ABC是直角三角形.…(4分)
∵圆M经过A,B,C三点,
∴圆M是Rt△ACB的外接圆.…(6分)
∴圆M的圆心M的坐标为AB的中点(2,3),半径r=
|AB|=1.
∴圆M的方程为(x-2)2+(y-3)2=1.…(8分)
(2)连接PM,则|PT|=
=
,…(10分)
∵|PO|=
,且|PT|=|PO|,
∴
=
,…(12分)
化简得2a+3b-6=0.
∴点P总在定直线2x+3y-6=0上.…(14分)
∵圆M经过三点A(2,2),B(2,4),C(3,3),
∴
|
解得
|
∴圆M的方程为(x-2)2+(y-3)2=1.…(8分)
解法二:设圆M的方程为(x-a)2+(y-b)2=r2(r>0),…(1分)
∵圆M经过三点A(2,2),B(2,4),C(3,3),
∴
|
解得
|
∴圆M的方程为(x-2)2+(y-3)2=1.…(8分)
解法三:∵A(2,2),B(2,4),
∴线段AB的垂直平分线方程为y=3,…(2分)
∵A(2,2),C(3,3),
∴线段AC的垂直平分线方程为y-
| 5 |
| 2 |
| 5 |
| 2 |
由
|
故圆M的半径r=|AM|=
| (2-2)2+(3-2)2 |
∴圆M的方程为(x-2)2+(y-3)2=1.…(8分)
解法四:∵|AB|=
| (2-2)2+(2-4)2 |
| (2-3)2+(2-3)2 |
| 2 |
| (2-3)2+(4-3)2 |
| 2 |
∴|AC|2+|BC|2=4=|AB|2.
∴△ABC是直角三角形.…(4分)
∵圆M经过A,B,C三点,
∴圆M是Rt△ACB的外接圆.…(6分)
∴圆M的圆心M的坐标为AB的中点(2,3),半径r=
| 1 |
| 2 |
∴圆M的方程为(x-2)2+(y-3)2=1.…(8分)
(2)连接PM,则|PT|=
| |PM|2-12 |
| (a-2)2+(b-3)2-1 |
∵|PO|=
| a2+b2 |
∴
| a2+b2 |
| (a-2)2+(b-3)2-1 |
化简得2a+3b-6=0.
∴点P总在定直线2x+3y-6=0上.…(14分)
点评:本题主要考查直线和圆等基本知识,考查运算求解能力和抽象概括能力,利用待定系数法,确定圆的方程是解题的关键.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
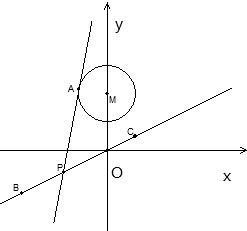 已知圆M:x2+(y-2)2=1,设点B,C是直线l:x-2y=0上的两点,它们的横坐标分别是t,t+4(t∈R),P点的纵坐标为a且点P在线段BC上,过P点作圆M的切线PA,切点为A
已知圆M:x2+(y-2)2=1,设点B,C是直线l:x-2y=0上的两点,它们的横坐标分别是t,t+4(t∈R),P点的纵坐标为a且点P在线段BC上,过P点作圆M的切线PA,切点为A