题目内容
有甲、乙两位射击运动员在一次射击测试中各射靶10次,他们每次命中环数的条形图如图所示,共计两位运动员的平均环数分别为 ,
, 标准差为
标准差为 ,
, ,则( ).
,则( ).
A. , , | B. , , |
C. , , | D. , ,  |
A
解析试题分析:甲乙两位射击运动员在一次射击测试中各射靶10次,根据两人每次射击的环数制成的条形图先分别求出 ,S甲和
,S甲和 ,S乙,再进行判断.解:甲乙两位射击运动员在一次射击测试中各射靶10次,根据两人每次射击的环数制成的条形图知:
,S乙,再进行判断.解:甲乙两位射击运动员在一次射击测试中各射靶10次,根据两人每次射击的环数制成的条形图知: =4×0.1+5×0.2+7×0.3+8×0.1+9×0.2+10×0.1=6.8, S甲=[
=4×0.1+5×0.2+7×0.3+8×0.1+9×0.2+10×0.1=6.8, S甲=[ (7-4)2×2+(7-5)2+(7-7)3×3+(7-8)2+(7-9)2×2+(7-10)2]=4,
(7-4)2×2+(7-5)2+(7-7)3×3+(7-8)2+(7-9)2×2+(7-10)2]=4, =5×0.1+6×0.2+7×0.4+8×0.2+9×0.1=7, S乙=
=5×0.1+6×0.2+7×0.4+8×0.2+9×0.1=7, S乙= [(7-5)2+(7-6)2×2+(7-7)2×4+(7-8)2×2+(7-9)2]=1.2,∴S甲>S乙,故选A.
[(7-5)2+(7-6)2×2+(7-7)2×4+(7-8)2×2+(7-9)2]=1.2,∴S甲>S乙,故选A.
考点:频率分布直方图
点评:本题考查频率分布直方图的应用,是基础题.解题时要认真审题,仔细解答

练习册系列答案
相关题目
观察新生婴儿的体重,其频率分布直方图如图所示,则新生婴儿体重在 的频率为 ( )
的频率为 ( )
| A.0.001 | B.0.1 | C.0.2 | D.0.3 |
废品率x%和每吨生铁成本y(元)之间的回归直线方程为y=256+3x,表明( )
| A.废品率每增加1%,生铁成本增加259元. | B.废品率每增加1%,生铁成本增加3元. |
| C.废品率每增加1%,生铁成本每吨增加3元. | D.废品率不变,生铁成本为256元. |
对两个变量 和
和 进行回归分析,得到一组样本数据:
进行回归分析,得到一组样本数据: ,则下列说法中不正确的是( )
,则下列说法中不正确的是( )
A.由样本数据得到的回归方程 必过样本中心 必过样本中心 |
| B.残差平方和越小的模型,拟合的效果越好 |
C.用相关指数 来刻画回归效果, 来刻画回归效果, 越小,说明模型的似合效果越好 越小,说明模型的似合效果越好 |
D.若变量y和x之间的相关系数为 ,则变量y和x之间具有线性相关关系 ,则变量y和x之间具有线性相关关系 |
为了解儿子身高与其父亲身高的关系,随机抽取5对父子身高数据如下
| 父亲身高x(cm) | 174 | 176 | 176 | 176 | 178 |
| 儿子身高y(cm) | 175 | 175 | 176 | 177 | 177 |
A.
 B.
B. C.
C. D.
D.
样本点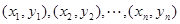 的样本中心与回归直线
的样本中心与回归直线 的关系( )
的关系( )
| A.在直线上 | B.在直线左上方 | C.在直线右下方 | D.在直线外 |




 等于
等于
















 ,现用分层抽样的方法从该校高中三个年级的学生中抽取容量为50的样本,则应从高二年级抽取( ) 名学生
,现用分层抽样的方法从该校高中三个年级的学生中抽取容量为50的样本,则应从高二年级抽取( ) 名学生