Question

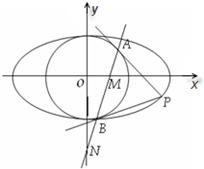已知椭圆

x2

a2

+

y2

b2

=1  (a＞b＞0)和圆O：x²+y²=b²，过椭圆上一点P引圆O的两条切线，切点分别为A，B．
（1）（ⅰ）若圆O过椭圆的两个焦点，求椭圆的离心率e；
（ⅱ）若椭圆上存在点P，使得∠APB=90°，求椭圆离心率e的取值范围；
（2）设直线AB与x轴、y轴分别交于点M，N，求证：

a2

|ON|2

+

b2

|OM|2

为定值．

Answer 1

分析：（Ⅰ）（ⅰ）由圆O过椭圆的焦点，知圆O：x²+y²=b²，由此能求出椭圆的离心率e；
      （ⅱ）由∠APB=90°及圆的性质，可得|OP|=

2

b，|OP|²=2b²≤a²，由此能求出椭圆离心率e的取值范围；
（Ⅱ）设P（x₀，y₀），A（x₁，y₁），B（x₂，y₂），则

y0-y1

x0-x1

=-

x1

y1

，所以PA方程为：x₁x+y₁y=b²，PB方程为：x₂x+y₂y=b²．由此入手能得到

a2

|ON|2

+

b2

|OM|2

为定值．

解答：解：（Ⅰ）（ⅰ）∵圆O过椭圆的焦点，圆O：x²+y²=b²，
∴b=c，∴b²=a²-c²=c²，∴a²=2c²，
∴e=

2

2

．（3分）
（ⅱ）由∠APB=90°及圆的性质，可得|OP|=

2

b，
∴|OP|²=2b²≤a²，∴a²≤2c²
∴e2≥

1

2

，

2

2

≤e＜1．（6分）
（Ⅱ）设P（x₀，y₀），A（x₁，y₁），B（x₂，y₂），则

y0-y1

x0-x1

=-

x1

y1

整理得x₀x+y₀y=x₁²+y₁²∵x₁²+y₁²=b²
∴PA方程为：x₁x+y₁y=b²，PB方程为：x₂x+y₂y=b²．
∴x₁x+y₁y=x₂x+y₂y，∴

y2-y1

x2-x1

=-

x0

y0

，
直线AB方程为y-y1=-

x0

y0

(x-x1)，即x₀x+y₀y=b²．
令x=0，得|ON|=|y|=

b2

|y0|

，令y=0，得|OM|=|x|=

b2

|x0|

，
∴

a2

|ON|2

+

b2

|OM|2

=

a2 y 2 0 +b2 x 2 0

b4

=

a2b2

b4

=

a2

b2

，
∴

a2

|ON|2

+

b2

|OM|2

为定值，定值是

a2

b2

．（12分）

点评：本题考查圆锥曲线的性质和应用，解题时要认真审题，仔细解答，注意公式的合理运用．