题目内容
已知函数f（x）=（-x2+ax）ex（a∈R）在[-1，1]上单调递增，求a的取值范围．
解：∵f（x）=（-x2+ax）ex（a∈R），
∴f′（x）=[-x2+（a-2）x+a]ex，令g（x）=-x2+（a-2）x+a，
又f（x）=（-x2+ax）ex（a∈R）在[-1，1]上单调递增，
∴当x∈[-1，1]时，f′（x）≥0，
∴
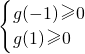，即
，解得a≥
．
∴a的取值范围为：a≥．
分析：可求得f′（x）=[-x2+（a-2）x+a]ex，利用x∈[-1，1]时，f′（x）≥0即可求得a的取值范围．
点评：本题考查利用导数研究函数的单调性，构造函数g（x）=-x2+（a-2）x+a，得到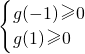是关键，考查理解与等价转化的能力，属于中档题．
∴f′（x）=[-x2+（a-2）x+a]ex，令g（x）=-x2+（a-2）x+a，
又f（x）=（-x2+ax）ex（a∈R）在[-1，1]上单调递增，
∴当x∈[-1，1]时，f′（x）≥0，
∴
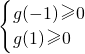，即，解得a≥．∴a的取值范围为：a≥
．分析：可求得f′（x）=[-x2+（a-2）x+a]ex，利用x∈[-1，1]时，f′（x）≥0即可求得a的取值范围．
点评：本题考查利用导数研究函数的单调性，构造函数g（x）=-x2+（a-2）x+a，得到
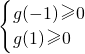是关键，考查理解与等价转化的能力，属于中档题． 
练习册系列答案
阅读快车系列答案
相关题目
已知函数f（x）=x2-bx的图象在点A（1，f（1））处的切线l与直线3x-y+2=0平行，若数列{
}的前n项和为Sn，则S2010的值为（ ）
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|