题目内容
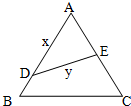 如图,江北水城湖畔有一块边长为2a的等边三角形的草坪,在这块草坪内安装灌溉水管DE,使DE把草坪分成面积相等的两部分,D在AB上,E在AC上.
如图,江北水城湖畔有一块边长为2a的等边三角形的草坪,在这块草坪内安装灌溉水管DE,使DE把草坪分成面积相等的两部分,D在AB上,E在AC上.
①设AD=x(x≥0),DE=y,求y关于x的函数关系式;
②为节约成本,应如何安装,才能使灌溉水管DE最短,最短是多少?
解:①∵ ,∴
,∴ ,
,
∴AE=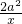 ,
,
在△ADE中, ,
,
∵y>0,∴
又AE=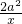 ≤2a,∴x≥a,∵D在AB上,∴x≤2a,
≤2a,∴x≥a,∵D在AB上,∴x≤2a,
∴ (a≤x≤2a)
(a≤x≤2a)
② ,
,
当且仅当 ,即
,即 时“=”成立,
时“=”成立,
此时 ,∴使AD=AE=
,∴使AD=AE= 时,DE最短,最短为
时,DE最短,最短为 .
.
分析:①先根据S△ADE= S△ABC求得x和AE的关系,进而根据余弦定理把x和AE的关系代入求得x和y的关系.
S△ABC求得x和AE的关系,进而根据余弦定理把x和AE的关系代入求得x和y的关系.
②根据均值不等式求得y的最小值,求得等号成立时的x的值即可.
点评:本题主要考查了基本不等式,以及函数的单调型求最值,考查了学生运用所学知识解决实际问题的能力,属于综合题.
 ,∴
,∴ ,
,∴AE=
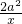 ,
,在△ADE中,
 ,
,∵y>0,∴

又AE=
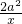 ≤2a,∴x≥a,∵D在AB上,∴x≤2a,
≤2a,∴x≥a,∵D在AB上,∴x≤2a,∴
 (a≤x≤2a)
(a≤x≤2a) ②
 ,
,当且仅当
 ,即
,即 时“=”成立,
时“=”成立,此时
 ,∴使AD=AE=
,∴使AD=AE= 时,DE最短,最短为
时,DE最短,最短为 .
.分析:①先根据S△ADE=
 S△ABC求得x和AE的关系,进而根据余弦定理把x和AE的关系代入求得x和y的关系.
S△ABC求得x和AE的关系,进而根据余弦定理把x和AE的关系代入求得x和y的关系.②根据均值不等式求得y的最小值,求得等号成立时的x的值即可.
点评:本题主要考查了基本不等式,以及函数的单调型求最值,考查了学生运用所学知识解决实际问题的能力,属于综合题.

练习册系列答案
相关题目
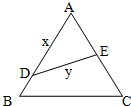 如图,江北水城湖畔有一块边长为2a的等边三角形的草坪,在这块草坪内安装灌溉水管DE,使DE把草坪分成面积相等的两部分,D在AB上,E在AC上.
如图,江北水城湖畔有一块边长为2a的等边三角形的草坪,在这块草坪内安装灌溉水管DE,使DE把草坪分成面积相等的两部分,D在AB上,E在AC上.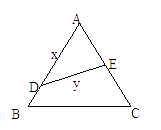 ②为节约成本,应如何安装,才能使灌溉水管DE最短,最短是多少?
②为节约成本,应如何安装,才能使灌溉水管DE最短,最短是多少?