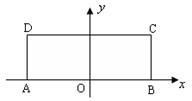
题目内容
如图,设P为长方形ABCD所在平面外一点,M、N分别为AB、PD上的点,且
思路分析:要证直线MN∥平面PBC,只需证明MN∥平面PBC内的一条直线或MN所在的某个平面∥平面PBC.
证法一:过N作NR∥DC交PC于点R,连结RB,依题意得 ![]() =
=![]() =
=![]() =
=![]() =
=![]()
![]() NR=MB.
NR=MB.
∵NR∥DC∥AB,
∴四边形MNRB是平行四边形.
∴MN∥RB.
又∵RB![]() 平面PBC,
平面PBC,
∴直线MN∥平面PBC.
证法二:过N作NQ∥AD交PA于点Q,连结QM,
∵![]() =
=![]() =
=![]() ,
,
∴QM∥PB.
又NQ∥AD∥BC,
∴平面MQN∥平面PBC.
∴直线MN∥平面PBC.
证法三:过N作NR∥DC交PC于点R,连结RB,依题意有![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,![]() =
=![]() +
+![]() +
+![]() =
=![]() .
.
∴MN∥RB.
又∵RB![]() 平面PBC,∴直线MN∥平面PBC.
平面PBC,∴直线MN∥平面PBC.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
 ,
,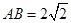 ,
,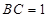 ,以
,以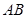 的中点
的中点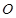 为
为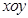 .
.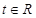 ,探究
,探究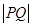 的最
的最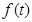 。
。