题目内容

已知函数f（x）=|x|（x+1），试画出函数f（x）的图象，并根据图象解决下列两个问题
（1）写出函数f（x）的单调区间；
（2）求函数f（x）在区间[-1， $数学公式$ 的最大值．

解：f（x）=|x|（x+1）= $\text{[math]}$ ，
当x＜0时，函数图象是开口向下的抛物线的一部分，
对称轴为直线x=- $\text{[math]}$ ，以（- $\text{[math]}$ ， $\text{[math]}$ ）为顶点；
当x＞0时，函数图象是开口向上的抛物线弧，
在（0，+∞）上为增函数，最小值为f（0）=0．
由此可得函数的图象如右图所示
（1）由函数的表达式，结合二次函数的性质，
可得f（x）在 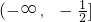$\text{[math]}$ 和[0，+∞]上递增，在 $\text{[math]}$ 上递减；
（2）∵函数f（x）在[-1，- $\text{[math]}$ ]上是增函数，在[- $\text{[math]}$ ，0]上减函数，在[0， $\text{[math]}$ ]上是增函数
∴函数的最大值是f（- $\text{[math]}$ ）与f（ $\text{[math]}$ ）中较大的那一个
∵ $\text{[math]}$ ， $\text{[math]}$
∴f（x）在区间[-1， $\text{[math]}$ ]的最大值为 $\text{[math]}$
分析：根据绝对值的意义，将函数化简为分段函数表达式：f（x）= $\text{[math]}$ ，从而得到函数图象是开口向下的抛物线在y轴的左侧的部分，和开口向上的抛物线在y轴右侧的部分拼接而成．
（1）根据二次函数的图象性质，结合我们作出的图象，不难得到函数在R上有三单调区间：增区间为 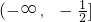$\text{[math]}$ 和[0，+∞]，减区间为 $\text{[math]}$ ；
（2）先讨论函数在区间[-1， $\text{[math]}$ 的单调性是先增后减，然后再增．由此可得函数的最大值是两个增区间的右端点函数值中较大的那个，计算函数值再比较大小，即可得这个最大值．
点评：本题借助于一个含有绝对值函数的图象的作法问题，着重考查了函数图象的作法、二次函数的图象与性质和函数最值等知识点，属于中档题．