题目内容
若m,n,m+n成等差数列,m,n,m•n成等比数列,则直线2mx+ny+1=0的倾斜角为
.
| 3π |
| 4 |
| 3π |
| 4 |
分析:由于m,n,m+n成等差数列,m,n,m•n成等比数列,可得2n=m+m+n,n2=m•mn,又mn≠0,解得m,n.再利用倾斜角与斜率的关系即可得出.
解答:解:∵m,n,m+n成等差数列,m,n,m•n成等比数列,
∴2n=m+m+n,n2=m•mn,又mn≠0,解得m=2,n=4.
∴直线2mx+ny+1=0可化为4x+4y+1=0.
设倾斜角为α,则tanα=-
=-1,解得α=
.
故答案为
.
∴2n=m+m+n,n2=m•mn,又mn≠0,解得m=2,n=4.
∴直线2mx+ny+1=0可化为4x+4y+1=0.
设倾斜角为α,则tanα=-
| 4 |
| 4 |
| 3π |
| 4 |
故答案为
| 3π |
| 4 |
点评:本题考查了等差数列、等比数列、直线的倾斜角与斜率的关系等基础知识与基本技能方法,属于基础题.

练习册系列答案
相关题目
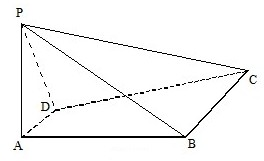 如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD是直角梯形,其中DA⊥AB,AD∥BC.PA=2AD=BC=2AB=2
如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD是直角梯形,其中DA⊥AB,AD∥BC.PA=2AD=BC=2AB=2