题目内容
已知实数x,y满足不等式组 且x2+y2的最大值等于a,最小值等于b,则a+b=________.
且x2+y2的最大值等于a,最小值等于b,则a+b=________.
39
分析:确定不等式组对应的平面区域为三角形的区域,明确目标函数的几何意义是点(x,y)到原点的距离的平方,即可求得结论.
解答: 解:由题意,不等式组确定一个三角形的区域,三角形的三个顶点的坐标为(5,3),(-1,3),(3,1),
解:由题意,不等式组确定一个三角形的区域,三角形的三个顶点的坐标为(5,3),(-1,3),(3,1),
原点到直线x+2y-5=0的距离为d= =
=
∵x2+y2的几何意义是点(x,y)到原点的距离的平方
∴x2+y2的最大值等于52+32=34,
最小值等于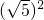 =5
=5
∵x2+y2的最大值等于a,最小值等于b,
∴a=34,b=5
∴a+b=39
故答案为:39
点评:本题考查线性规划知识的运用,解题的关键是确定不等式组对应的平面区域,明确目标函数的几何意义.
分析:确定不等式组对应的平面区域为三角形的区域,明确目标函数的几何意义是点(x,y)到原点的距离的平方,即可求得结论.
解答:
 解:由题意,不等式组确定一个三角形的区域,三角形的三个顶点的坐标为(5,3),(-1,3),(3,1),
解:由题意,不等式组确定一个三角形的区域,三角形的三个顶点的坐标为(5,3),(-1,3),(3,1),原点到直线x+2y-5=0的距离为d=
 =
=
∵x2+y2的几何意义是点(x,y)到原点的距离的平方
∴x2+y2的最大值等于52+32=34,
最小值等于
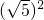 =5
=5∵x2+y2的最大值等于a,最小值等于b,
∴a=34,b=5
∴a+b=39
故答案为:39
点评:本题考查线性规划知识的运用,解题的关键是确定不等式组对应的平面区域,明确目标函数的几何意义.

练习册系列答案
相关题目
 ,则目标函数z=x-y的最大值等于( )
,则目标函数z=x-y的最大值等于( )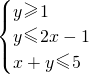 ,则目标函数z=x-y的最大值等于________.
,则目标函数z=x-y的最大值等于________. ,则目标函数z=x-y的最大值等于 .
,则目标函数z=x-y的最大值等于 .