题目内容
已知函数![]() ,在点
,在点![]() 处的切线方程为
处的切线方程为![]() .
.
(1)求函![]() 数
数![]() 的解析式;
的解析式;
(2)若对于区间![]() 上任意两个自变量的值
上任意两个自变量的值![]() ,都有
,都有![]() ,求实数
,求实数![]() 的最小值;
的最小值;
(3)若过点![]() ,可作曲线
,可作曲线![]() 的三条切线,求实数
的三条切线,求实数![]() 的取值范围。
的取值范围。
解答:(1)![]() …………1分
…………1分
根据题意,得![]() 即
即![]()
解得![]()
![]() …………3分
…………3分
(2)令![]()
![]() ,解得
,解得![]()
f(-1)=2, f(1)=-2,![]()
![]() 时,
时,![]() …………5分
…………5分
则对于区间[-2,2]上任意两个自变量的值![]() ,都有
,都有
![]()
所以![]() 所以
所以![]() 的最小值为4。 …………7分
的最小值为4。 …………7分
(3)设切点为![]()
![]() ,
, ![]() 切线的斜率为
切线的斜率为![]() …………8分
…………8分
则![]()
即![]() , …………
, …………![]() 9分
9分
因为过点![]() ,可作曲线
,可作曲线![]() 的三条切线
的三条切线
所以方程![]() 有三个不同的实数解
有三个不同的实数解
即函数![]() 有三个不同的零点, …………10分
有三个不同的零点, …………10分
则![]()
令![]()
|
|
| 0 | (0,2) | 2 | (2,+∞) |
|
| + | 0 | — | 0 | + |
|
|
| 极大值 |
| 极小值 |
|
…………12分
![]() 即
即![]() ,∴
,∴![]() …………14分
…………14分

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
 (
( ).
).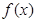 的单调区间;
的单调区间; 的图象为曲线
的图象为曲线 .设点
.设点 ,
, 是曲线
是曲线 ,使得:①
,使得:① ;②曲线
;②曲线 处的切线平行
处的切线平行 ,则称函数
,则称函数 存在“中值相依切线”.试问:函数
存在“中值相依切线”.试问:函数