题目内容
设地球的半径为R,地球上A、B两地都在北纬45°的纬度线上,且其经度差为90°,则A、B两地的球面距离是
R
R.
| π |
| 3 |
| π |
| 3 |
分析:设在北纬45°的纬圆的圆心为C,球心为O,连结OA、OB、OC、AC、BC.根据地球纬度的定义,算出小圆半径AC=BC=
.由A、B两地经度差为90°,在Rt△ABC中算出AB=
=R,从而得到∠AOB=60°,利用球面距离的公式加以计算,即可得到A、B两地的球面距离.
| ||
| 2 |
| AC2+BC2 |
解答:解: 设在北纬45°的纬圆的圆心为C,球心为O,
设在北纬45°的纬圆的圆心为C,球心为O,
连结OA、OB、OC、AC、BC,则OC⊥平面ABC
Rt△ACO中,AC=OAcos45°=
,同理BC=
,
∵A、B两地经度差为90°,
∴∠ACB=90°,Rt△ABC中,AB=
=R
由此可得△AOB是边长为R的等边三角形,得∠AOB=60°
∴A、B两地的球面距离是
=
R.
故答案为:
R
 设在北纬45°的纬圆的圆心为C,球心为O,
设在北纬45°的纬圆的圆心为C,球心为O,连结OA、OB、OC、AC、BC,则OC⊥平面ABC
Rt△ACO中,AC=OAcos45°=
| ||
| 2 |
| ||
| 2 |
∵A、B两地经度差为90°,
∴∠ACB=90°,Rt△ABC中,AB=
| AC2+BC2 |
由此可得△AOB是边长为R的等边三角形,得∠AOB=60°
∴A、B两地的球面距离是
| 60πR |
| 180 |
| π |
| 3 |
故答案为:
| π |
| 3 |
点评:本题求地球上北纬45度圈上两点的球面距离,着重考查了球面距离及相关计算、经纬度等基础知识,考查运算求解能力,考查空间想象能力,属于基础题.

练习册系列答案
相关题目
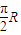 ,若A地为东经0°,则B地的经度为 .
,若A地为东经0°,则B地的经度为 .