题目内容
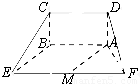
如图五面体中，平面ABCD⊥平面BFEC，AB=AD=BF=EF=1，CB=CD=CE=| 3 |
（1）证明：AF∥DE；
（2）求二面角E-AD-B的余弦值．
分析：（1）证明AF∥DE，利用面面平行的性质定理进行证明，只需证明AB∥平面DEM，BF∥平面DEM即可；
（2）作MN⊥AD，垂足为N，连接EN，则EN⊥AD，可得∠ENM为所求二面角的平面角，在△DMN中可求．
（2）作MN⊥AD，垂足为N，连接EN，则EN⊥AD，可得∠ENM为所求二面角的平面角，在△DMN中可求．
解答：
（1）证明：∵平面ABCD⊥平面BFEC，AB⊥BC，平面ABCD∩平面BFEC=BC，
∴AB⊥平面BFEC
∵FB?平面BFEC
∴AF⊥FB
∵AB⊥BC，FB⊥BC，∴四边形ABCD和四边形BCEF中∠BCD=∠BCE=60°
过D作DM⊥BC于M，连接EM，在△DMC和△EMC中，∠MCD=∠MCE=60°，CD=CE，CM=CM
∴△DMC≌△EMC
∴∠DMC=∠EMC=90°
∴EM⊥BC
∵AB⊥BC，FB⊥BC
∴EM∥BF，DM∥AB
∵EM，DM?平面DEM，BF，AB?平面DEM
∴AB∥平面DEM，BF∥平面DEM
∵AB∩BF=B
∴平面ABF∥平面DEM
∵平面ADEF与平面ABF、平面DEM的交线分别为AF，DE
∴AF∥DE；
（2）解：作MN⊥AD，垂足为N，连接EN，则EN⊥AD，所以∠ENM为所求二面角的平面角
由（1）知EM=MD=
，在△DMN中，MN=
，∴tan∠ENM=
∴cos∠ENM=
（1）证明：∵平面ABCD⊥平面BFEC，AB⊥BC，平面ABCD∩平面BFEC=BC，∴AB⊥平面BFEC
∵FB?平面BFEC
∴AF⊥FB
∵AB⊥BC，FB⊥BC，∴四边形ABCD和四边形BCEF中∠BCD=∠BCE=60°
过D作DM⊥BC于M，连接EM，在△DMC和△EMC中，∠MCD=∠MCE=60°，CD=CE，CM=CM
∴△DMC≌△EMC
∴∠DMC=∠EMC=90°
∴EM⊥BC
∵AB⊥BC，FB⊥BC
∴EM∥BF，DM∥AB
∵EM，DM?平面DEM，BF，AB?平面DEM
∴AB∥平面DEM，BF∥平面DEM
∵AB∩BF=B
∴平面ABF∥平面DEM
∵平面ADEF与平面ABF、平面DEM的交线分别为AF，DE
∴AF∥DE；
（2）解：作MN⊥AD，垂足为N，连接EN，则EN⊥AD，所以∠ENM为所求二面角的平面角
由（1）知EM=MD=
| 3 |
| 2 |
3
| ||
| 4 |
2
| ||
| 3 |
∴cos∠ENM=
| ||
| 7 |
点评：本题考查线线平行，考查面面角，解题的关键是掌握面面、线面平行的判定，正确找出面面角．
练习册系列答案
相关题目
如图所示的五面体中，四边形ABCD是矩形，DA⊥面ABEF，且DA=1，AB∥EF，AB=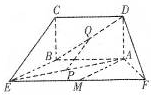
如图，五面体中，四边形ABCD是矩形，DA⊥面ABEF，且DA=1，AB∥EF，AB=
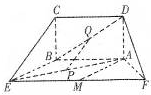如图，五面体中，四边形ABCD是矩形，DA⊥面ABEF，且DA=1，AB∥EF，
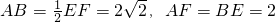，P、Q、M分别为AE、BD、EF的中点．
EF＝2
，AF＝BE＝2．
EF=2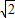
，AF=BE=2．