题目内容
已知数列{an}满足:a1=2,a n+1=2an+2.
(Ⅰ)求证:数列{an+2}是等比数列(要求指出首项与公比);
(Ⅱ)求数列{an}的前n项和Sn.
(Ⅰ)求证:数列{an+2}是等比数列(要求指出首项与公比);
(Ⅱ)求数列{an}的前n项和Sn.
证明:(Ⅰ)由an+1=2an+2,得an+1+2=2an+4, 即an+1+2=2(an+2),
∴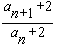 =2,n∈N*,
=2,n∈N*,
又由a1=2得a1+2=4,
所以数列{an+2}是以4为首项,以2为公比的等比数列.
(Ⅱ)由(Ⅰ)知an+2=4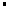 2 n﹣1=2 n+1,所以an=2 n+1﹣2,所以
2 n﹣1=2 n+1,所以an=2 n+1﹣2,所以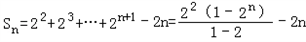 =2n+2﹣2n﹣4.
=2n+2﹣2n﹣4.
∴
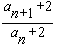 =2,n∈N*,
=2,n∈N*,又由a1=2得a1+2=4,
所以数列{an+2}是以4为首项,以2为公比的等比数列.
(Ⅱ)由(Ⅰ)知an+2=4
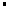 2 n﹣1=2 n+1,所以an=2 n+1﹣2,所以
2 n﹣1=2 n+1,所以an=2 n+1﹣2,所以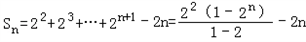 =2n+2﹣2n﹣4.
=2n+2﹣2n﹣4.
练习册系列答案
相关题目