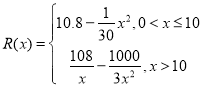题目内容
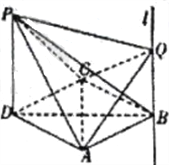
【题目】四棱锥![]() 中,
中,![]() 面
面![]() ,底面
,底面![]() 是菱形,且
是菱形,且![]() ,
,![]() ,过点
,过点![]() 作直线
作直线![]() ,
,![]() 为直线
为直线![]() 上一动点.
上一动点.
(1)求证:![]() ;
;
(2)当面![]() 面
面![]() 时,求三棱锥
时,求三棱锥![]() 的体积.
的体积.
【答案】(1)证明见解析;(2)![]() .
.
【解析】分析:(1)由![]() 平面
平面![]() 得
得![]() ,又在菱形
,又在菱形![]() 中有
中有![]() ,故得
,故得![]() 平面
平面![]() ,于是得到
,于是得到![]() .(2)结合题意可得
.(2)结合题意可得![]() 平面
平面![]() ,故
,故![]() .根据面
.根据面![]() 面
面![]() 得到
得到![]() ,然后根据几何图形的计算得到
,然后根据几何图形的计算得到![]() ,于是
,于是![]() ,
,![]() ,又
,又![]() ,由此可得所求的三棱锥的体积.
,由此可得所求的三棱锥的体积.
详解:(1)∵![]() ,
,
∴直线![]() 确定一平面
确定一平面![]() .
.
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() .
.
由题意知直线![]() 在面
在面![]() 上的射影为
上的射影为![]() ,
,
又在菱形![]() 中有
中有![]() ,
,![]() ,
,
∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,
,
∴![]() .
.
(2)由题意得![]() 和
和![]() 都是以
都是以![]() 为底的等腰三角形,设
为底的等腰三角形,设![]() 和
和![]() 的交点为
的交点为![]() ,
,
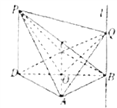
连接![]() 、
、![]() ,则
,则![]() ,
,![]() ,
,
又![]() ,
,
∴![]() 平面
平面![]() .
.
又平面![]() 面
面![]() ,平面
,平面![]()
![]()
![]() 面
面![]() ,
,
∴![]() 面
面![]() ,
,
∴![]() .
.
在菱形![]() 中,
中,![]() ,
,![]() ,
,
∴![]() .
.
在![]() 中,
中,![]() .
.
在![]() 中,设
中,设![]() ,则
,则![]() .
.
∴在![]() 中,
中,![]() ,
,
又在直角梯形![]() 中,
中,![]() ,
,
故![]() ,
,
解得![]() ,即
,即![]() .
.
∴![]() ,
,![]()
∴![]() .
.

【题目】某中学为调查该校学生每周参加社会实践活动的情况,随机收集了若干名学生每周参加社会实践活动的时间(单位:小时),将样本数据绘制如图所示的频率分布直方图,且在[0,2)内的学生有1人.
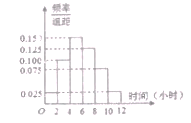
(1)求样本容量![]() ,并根据频率分布直方图估计该校学生每周参加社会实践活动时间的平均值;
,并根据频率分布直方图估计该校学生每周参加社会实践活动时间的平均值;
(2)将每周参加社会实践活动时间在[4,12]内定义为“经常参加社会实践”,参加活动时间在[0,4)内定义为“不经常参加社会实践”.已知样本中所有学生都参加了青少年科技创新大赛,有13人成绩等级为“优秀”,其余成绩为“一般”,其中成绩优秀的13人种“经常参加社会实践活动”的有12人.请将2×2列联表补充完整,并判断能否在犯错误的概率不超过0.05的前提下认为青少年科技创新大赛成绩“优秀”与经常参加社会实践活动有关;
(3)在(2)的条件下,如果从样本中“不经常参加社会实践”的学生中随机选取两人参加学校的科技创新班,求其中恰好一人成绩优秀的概率.
参考公式和数据:
![]() .
.
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |