题目内容
倾斜角为60°的一束平行光线,将一个半径为
的球投影在水平地面上,形成一个椭圆,则此椭圆的离心率为
.
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
分析:在平行光线照射过程中,椭圆的短半轴长是圆的半径,如图,椭圆的长半轴长是DE,过D向AE做垂线,垂足是C,得到一个直角三角形,得到DE的长,从而得出要求的结果.
解答: 解:在照射过程中,椭圆的短半轴长b是圆的半径R,
解:在照射过程中,椭圆的短半轴长b是圆的半径R,
∴b=
,如图.
椭圆的长轴长2a是DE,过D向AE做垂线,垂足是C,
由题意得:DC=2R=2
,∠CED=60°,
∴可得:DE=DC÷sin60°=2
÷
=4.
即2a=4,a=2,
∴椭圆的离心率为e=
=
=
=
故答案为:
.
 解:在照射过程中,椭圆的短半轴长b是圆的半径R,
解:在照射过程中,椭圆的短半轴长b是圆的半径R,∴b=
| 3 |
椭圆的长轴长2a是DE,过D向AE做垂线,垂足是C,
由题意得:DC=2R=2
| 3 |
∴可得:DE=DC÷sin60°=2
| 3 |
| ||
| 2 |
即2a=4,a=2,
∴椭圆的离心率为e=
| c |
| a |
| ||
| a |
| ||
| 2 |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查圆锥曲线的实际背景及作用,解决本题的关键是看清楚在平行光线的照射下,投影时球的有关量中,变与不变的量.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的球投影在水平地面上,形成一个椭圆,则此椭圆的离心率为________.
的球投影在水平地面上,形成一个椭圆,则此椭圆的离心率为________.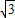 的球投影在水平地面上,形成一个椭圆,则此椭圆的离心率为 .
的球投影在水平地面上,形成一个椭圆,则此椭圆的离心率为 .