题目内容
已知Sn=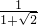 +
+ +
+ +…+
+…+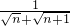 .若Sm=9,则m=________.
.若Sm=9,则m=________.
99
分析:先研究通项: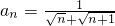 =
= ,然后令n=1,n=2,n=3,…,n=m,得到数列{an}的前m项的表达式,然后将这m项相加,可得Sm=
,然后令n=1,n=2,n=3,…,n=m,得到数列{an}的前m项的表达式,然后将这m项相加,可得Sm=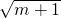 -1=9,从而得出m=99.
-1=9,从而得出m=99.
解答:设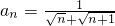
= =
=
∴ …(1)
…(1)
 …(2)
…(2)
 …(3)
…(3)
…
 …(m)
…(m)
将此m个式子相加,得
Sm=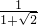 +
+ +
+ +…+
+…+
=( )+(
)+( )+…+(
)+…+( )
)
=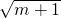 -1.
-1.
∵Sm=9,
∴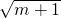 -1=9?m=99
-1=9?m=99
故答案为:99
点评:本题给出一个特殊的数列,在已知前m项的和的情况下,求正整数m的值,着重考查了数列求和中裂项累加的方法,属于中档题.
分析:先研究通项:
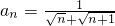 =
= ,然后令n=1,n=2,n=3,…,n=m,得到数列{an}的前m项的表达式,然后将这m项相加,可得Sm=
,然后令n=1,n=2,n=3,…,n=m,得到数列{an}的前m项的表达式,然后将这m项相加,可得Sm=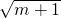 -1=9,从而得出m=99.
-1=9,从而得出m=99.解答:设
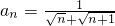
=
 =
=
∴
 …(1)
…(1) …(2)
…(2) …(3)
…(3)…
 …(m)
…(m)将此m个式子相加,得
Sm=
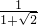 +
+ +
+ +…+
+…+
=(
 )+(
)+( )+…+(
)+…+( )
)=
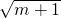 -1.
-1.∵Sm=9,
∴
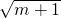 -1=9?m=99
-1=9?m=99故答案为:99
点评:本题给出一个特殊的数列,在已知前m项的和的情况下,求正整数m的值,着重考查了数列求和中裂项累加的方法,属于中档题.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目