题目内容

若曲线ρ=2
2
上有n个点到曲线ρ•cos(θ+
π
4
)=
2
的距离等于
2
，则n=（　　）
分析：分别化圆和直线的极坐标方程为直角坐标方程，然后利用数形结合分析曲线ρ=2
2
上有几个点到曲线ρ•cos(θ+
π
4
)=
2
的距离等于
2
．
解答：解：由ρ=2
2
，得ρ2=8，即x2+y2=8．
由ρ•cos(θ+
π
4
)=
2
，得ρcosθcos
π
4
-ρsinθsin
π
4
=
2
，
即
2
2
x-
2
2
y=
2
，x-y=2．
作出圆与直线方程如图，

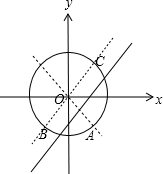
∵圆O的半径为2
2
，O到直线x-y=2的距离为
|2|
2
=
2
，
∴过O点与直线x-y=2平行的直线与圆的交点B、C和过O点与直线x-y=2垂直的直线与圆的交点A
满足到直线x-y=2的距离为
2
．
故选：C．
点评：本题考查了简单曲线的极坐标方程，考查了直线与圆的位置关系，体现了数形结合的解题思想方法，是基础题．
练习册系列答案
相关题目
已知椭圆C1的中心和抛物线C2的顶点都在原点，且两曲线的焦点均在x轴上，若A（1，2），B（2，0），C(
2
，
2
2
)中有两点在椭圆C1上，另一点在抛物线C2上．
（Ⅰ）求椭圆C1和抛物线C2的方程；
（Ⅱ）设直线l与椭圆C1交于M，N两点，与抛物线C2交于P，Q两点．问是否存在直线l使得以线段MN为直径的圆和以线段PQ为直径的圆都过原点？若存在，求出直线l的方程；若不存在，请说明理由．
已知函数y=x3+3x2+x的图象C上存在一定点P满足：若过点P的直线l与曲线C交于不同于P的两点M（x1，y1），N（x2，y2），就恒有y1+y2的定值为y0，则y0的值为
2
2
．
（2012•泉州模拟）（1）选修4-2：矩阵与变换
若二阶矩阵M满足M
12
34
=
710
46
．
（Ⅰ）求二阶矩阵M；
（Ⅱ）把矩阵M所对应的变换作用在曲线3x2+8xy+6y2=1上，求所得曲线的方程．
（2）选修4-4：坐标系与参数方程
已知在直角坐标系xOy中，曲线C的参数方程为
x=2tcosθ
y=2sinθ
（t为非零常数，θ为参数），在极坐标系（与直角坐标系xOy取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴）中，直线l的方程为ρsin(θ-
π
4
)=2
2
．
（Ⅰ）求曲线C的普通方程并说明曲线的形状；
（Ⅱ）是否存在实数t，使得直线l与曲线C有两个不同的公共点A、B，且
OA
•
OB
=10（其中O为坐标原点）？若存在，请求出；否则，请说明理由．
（3）选修4-5：不等式选讲
已知函数f（x）=|x-2|+|x-4|的最小值为m，实数a，b，c，n，p，q满足a2+b2+c2=n2+p2+q2=m．
（Ⅰ）求m的值；
（Ⅱ）求证：
n4
a2
+
p4
b2
+
q4
c2
≥2．
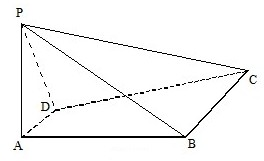精英家教网如图，四棱锥P-ABCD中，PA⊥平面ABCD，四边形ABCD是直角梯形，其中DA⊥AB，AD∥BC．PA=2AD=BC=2AB=2
2
．
（1）求异面直线PC与AD所成角的大小；
（2）若平面ABCD内有一经过点C的曲线E，该曲线上的任一动点Q都满足PQ与AD所成角的大小恰等PC与AD所成角．试判断曲线E的形状并说明理由；
（3）在平面ABCD内，设点Q是（2）题中的曲线E在直角梯形ABCD内部（包括边界）的一段曲线CG上的动点，其中G为曲线E和DC的交点．以B为圆心，BQ为半径的圆分别与梯形的边AB、BC交于M、N两点．当Q点在曲线段GC上运动时，试提出一个研究有关四面P-BMN的问题（如体积、线面、面面关系等）并尝试解决．
（说明：本小题将根据你提出的问题的质量和解决难度分层评分；本小题的计算结果可以使用近似值，保留3位小数）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网