题目内容
 在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,EC⊥AC,EF∥AC,AB=
在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,EC⊥AC,EF∥AC,AB= ,EF=EC=1,
,EF=EC=1,
(1)求证:平面BEF⊥平面DEF;
(2)求二面角A-BF-E的大小.
 解:(1)∵平面ACEF⊥平面ABCD,
解:(1)∵平面ACEF⊥平面ABCD,EC⊥AC,∴EC⊥平面ABCD;
建立如图所示的空间直角坐标系

 ,
,∴

设平面BEF、平面DEF的法向量分别为
 ,
,则
 =0①
=0① +1=0②
+1=0② =0③
=0③ +1=0④
+1=0④由①②③④解得x1=-
 ;x2=
;x2= ,
,∴

∴

 ,∴
,∴ ,
,故平面BEF⊥平面DEF
(2)设平面ABF的法向量
 ,∵
,∵
∴
 +1=0,
+1=0,
∴

∴cos<

由图知,二面角A-BF-E的平面角是钝角,
故所求二面角的大小为:π-arccos
 .
.分析:(1)以点C为坐标原点,CD为x轴,CB为y轴,CE为z轴,建立空间直角坐标系,然后分别求出平面BEF、平面DEF的法向量分别,根据法向量的数量积为0可得结论;
(2)先求出平面ABF的法向量然后求出与平面BEF的法向量的夹角,根据图形可知二面角A-BF-E的平面角是钝角,从而求出二面角的大小.
点评:本题主要考查了面面垂直的判定,以及二面角大小的度量,同时考查了推理能力、计算能力,以及应用向量知识解决立体几何问题的能力.

练习册系列答案
相关题目
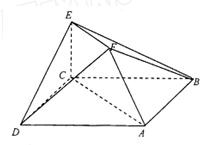 在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,EC⊥AC,EF∥AC,AB=
在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,EC⊥AC,EF∥AC,AB=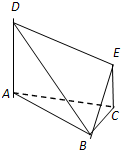 在如图所示的多面体中,底面△ABC是边长为2的正三角形,DA和EC均垂直于平面ABC,且DA=2,EC=1.
在如图所示的多面体中,底面△ABC是边长为2的正三角形,DA和EC均垂直于平面ABC,且DA=2,EC=1.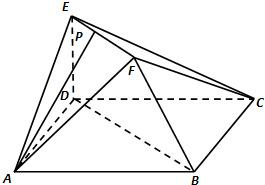 在如图所示的多面体中,已知正方形ABCD和
在如图所示的多面体中,已知正方形ABCD和 (2012•日照一模)在如图所示的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点.
(2012•日照一模)在如图所示的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点. 在如图所示的多面体中,AA1∥BB1,CC1⊥AC,CC1⊥BC.
在如图所示的多面体中,AA1∥BB1,CC1⊥AC,CC1⊥BC.