题目内容
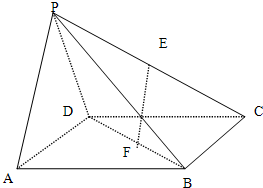 (2012•东莞二模)如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且PA=PD=
(2012•东莞二模)如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且PA=PD=
| ||
| 2 |
(1)求证:EF∥平面PAD;
(2)求证:平面PDC⊥平面PAD.
(3)求四棱锥P-ABCD的体积VP-ABCD.
分析:(1)连接AC,利用三角形中位线的性质,证明EF∥PA,利用线面平行的判定,可得EF∥平面PAD;
(2)面面垂直的性质,证明CD⊥平面PAD,进而可证平面PAD⊥平面PDC;
(3)先计算P-ADC的体积,再计算求四棱锥P-ABCD的体积VP-ABCD.
(2)面面垂直的性质,证明CD⊥平面PAD,进而可证平面PAD⊥平面PDC;
(3)先计算P-ADC的体积,再计算求四棱锥P-ABCD的体积VP-ABCD.
解答: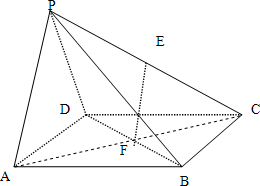 (1)证明:连接AC,则F是AC的中点,在△CPA中,EF∥PA,…(2分)
(1)证明:连接AC,则F是AC的中点,在△CPA中,EF∥PA,…(2分)
∵PA?平面PAD,EF?平面PAD,
∴EF∥平面PAD …(4分)
(2)证明:因为平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
又CD⊥AD,所以CD⊥平面PAD,…(7分)
又CD?平面PDC,∴平面PAD⊥平面PDC.…(8分)
(3)解:∵PA=PD=
AD=
,∴PA2+PD2=AD2,
∴PA⊥PD,S△PAD=
(
)2=1,…(10分)
又由(2)可知CD⊥平面PAD,CD=2,…(11分)
∴VP-ADC=VC-PAD=
×1×2=
,…(13分)
∴VP-ABCD=2VP-ADC=2×
=
.…(14分)
 (1)证明:连接AC,则F是AC的中点,在△CPA中,EF∥PA,…(2分)
(1)证明:连接AC,则F是AC的中点,在△CPA中,EF∥PA,…(2分)∵PA?平面PAD,EF?平面PAD,
∴EF∥平面PAD …(4分)
(2)证明:因为平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
又CD⊥AD,所以CD⊥平面PAD,…(7分)
又CD?平面PDC,∴平面PAD⊥平面PDC.…(8分)
(3)解:∵PA=PD=
| ||
| 2 |
| 2 |
∴PA⊥PD,S△PAD=
| 1 |
| 2 |
| 2 |
又由(2)可知CD⊥平面PAD,CD=2,…(11分)
∴VP-ADC=VC-PAD=
| 1 |
| 3 |
| 2 |
| 3 |
∴VP-ABCD=2VP-ADC=2×
| 2 |
| 3 |
| 4 |
| 3 |
点评:本题考查线面平行,考查面面垂直,考查棱锥体积的计算,解题的关键是掌握线面平行,面面垂直的判定,正确运用棱锥的体积公式,属于中档题.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
 (2012•东莞二模)甲、乙两名运动员的5次测试成绩如图所示,设s1,s2分别表示甲、乙两名运动员测试成绩的标准差,
(2012•东莞二模)甲、乙两名运动员的5次测试成绩如图所示,设s1,s2分别表示甲、乙两名运动员测试成绩的标准差,