题目内容
在平面直角坐标系xOy中,过定点C(0,p)作直线与抛物线x2=2py(p>0)相交于A、B两点.(Ⅰ)若点N是点C关于坐标原点O的对称点,求△ANB面积的最小值;
(Ⅱ)是否存在垂直于y轴的直线l,使得l被以AC为直径的圆截得弦长恒为定值?若存在,求出l的方程;若不存在,说明理由.
分析:解法1:(Ⅰ)依题意,点N的坐标为N(0,-p),可设A(x1,y1),B(x2,y2),直线AB的方程为y=kx+p,与x2=2py联立得
消去y得x2-2pkx-2p2=0.然后由韦达定理结合三角形面积公式进行求解.
(Ⅱ)假设满足条件的直线l存在,其方程为y=a,AC的中点为O',l与AC为直径的圆相交于点P,Q,PQ的中点为H,
则O'H⊥PQ,Q'点的坐标为(
,y1+
),由此入手能够求出抛物线的通径所在的直线.
解法2:(Ⅰ)依题意,点N的坐标为N(0,-p),可设A(x1,y1),B(x2,y2),直线AB的方程为y=kx+p,与x2=2py联立得
消去y得x2-2pkx-2p2=0.由弦长公式得|AB|=
|x1-x2|=
•
=
•
=2p
•
,又由点到直线的距离公式得d=
.由此能求出△ANB面积的最小值.
(Ⅱ)假设满足条件的直线l存在,其方程为y=a,则以AC为直径的圆的方程为(x-0)(x-x1)-(y-p)(y-y1)=0,
将直线方程y=a代入得x2-x1x+(a-p)(a-y1)=0,则△=
-4(a-p)(a-y1)=4[(a-
)y1+a(p-a)].由此入手能够求出抛物线的通径所在的直线.
|
(Ⅱ)假设满足条件的直线l存在,其方程为y=a,AC的中点为O',l与AC为直径的圆相交于点P,Q,PQ的中点为H,
则O'H⊥PQ,Q'点的坐标为(
| x1 |
| 2 |
| p |
| 2 |
解法2:(Ⅰ)依题意,点N的坐标为N(0,-p),可设A(x1,y1),B(x2,y2),直线AB的方程为y=kx+p,与x2=2py联立得
|
| 1+k2 |
| 1+k2 |
| (x1+x2)2-4x1x2 |
| 1+k2 |
| 4p2k2+8p2 |
| 1+k2 |
| k2+2 |
| 2p | ||
|
(Ⅱ)假设满足条件的直线l存在,其方程为y=a,则以AC为直径的圆的方程为(x-0)(x-x1)-(y-p)(y-y1)=0,
将直线方程y=a代入得x2-x1x+(a-p)(a-y1)=0,则△=
| x | 2 1 |
| p |
| 2 |
解答: 解:法1:(Ⅰ)依题意,点N的坐标为N(0,-p),
解:法1:(Ⅰ)依题意,点N的坐标为N(0,-p),
可设A(x1,y1),B(x2,y2),
直线AB的方程为y=kx+p,与x2=2py联立得
,
消去y得x2-2pkx-2p2=0.
由韦达定理得x1+x2=2pk,x1x2=-2p2.
于是S△ABN=S△BCN+S△ACN=
•2p|x1-x2|
=p|x1-x2|=p
=p
=2p2
,
∴当k=0时,(S△ABN)min=2
p2.
(Ⅱ)假设满足条件的直线l存在,其方程为y=a,
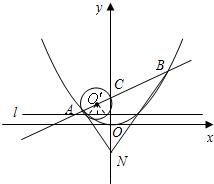 AC的中点为O',l与AC为直径的圆相交于点P,Q,PQ的中点为H,
AC的中点为O',l与AC为直径的圆相交于点P,Q,PQ的中点为H,
则O'H⊥PQ,Q'点的坐标为(x1,
).
∵|O′P|=
|AC|=
=
,|O′H|=|a-
|=
|2a-y1-p|,
∴|PH|2=|O'P|2-|O'H|2=
(
+p2)-
(2a-y1-p)2=(a-
)y1+a(p-a),
∴|PQ|2=(2|PH|)2=4[(a-
)y1+a(p-a)].
令a-
=0,得a=
,此时|PQ|=p为定值,
故满足条件的直线l存在,其方程为y=
,
即抛物线的通径所在的直线.
解法2:(Ⅰ)前同解法1,再由弦长公式得|AB|=
|x1-x2|=
•
=
•
=2p
•
,
又由点到直线的距离公式得d=
.
从而S△ABN=
?d•|AB|=
•2p
•
•
=2p2
,∴当k=0时,(S△ABN)min=2
p2.
(Ⅱ)假设满足条件的直线l存在,其方程为y=a,则以AC为直径的圆的方程为(x-0)(x-x1)+(y-p)(y-y1)=0,
将直线方程y=a代入得x2-x1x+(a-p)(a-y1)=0,
则|x1-x2|2=
-4(a-p)(a-y1)=4[(a-
)y1+a(p-a)].
设直线l与以AC为直径的圆的交点为P(x3,y3),Q(x4,y4),
则有|PQ|=|x3-x4|=
=2
.
令a-
=0,得a=
,此时|PQ|=p为定值,故满足条件的直线l存在,其方程为y=
,
即抛物线的通径所在的直线.
 解:法1:(Ⅰ)依题意,点N的坐标为N(0,-p),
解:法1:(Ⅰ)依题意,点N的坐标为N(0,-p),可设A(x1,y1),B(x2,y2),
直线AB的方程为y=kx+p,与x2=2py联立得
|
消去y得x2-2pkx-2p2=0.
由韦达定理得x1+x2=2pk,x1x2=-2p2.
于是S△ABN=S△BCN+S△ACN=
| 1 |
| 2 |
=p|x1-x2|=p
| (x1+x2)2-4x1x2 |
=p
| 4p2k2+8p2 |
| k2+2 |
∴当k=0时,(S△ABN)min=2
| 2 |
(Ⅱ)假设满足条件的直线l存在,其方程为y=a,
 AC的中点为O',l与AC为直径的圆相交于点P,Q,PQ的中点为H,
AC的中点为O',l与AC为直径的圆相交于点P,Q,PQ的中点为H,则O'H⊥PQ,Q'点的坐标为(x1,
| y1+p |
| 2 |
∵|O′P|=
| 1 |
| 2 |
| 1 |
| 2 |
|
| 1 |
| 2 |
|
| y1+p |
| 2 |
| 1 |
| 2 |
∴|PH|2=|O'P|2-|O'H|2=
| 1 |
| 4 |
| y | 2 1 |
| 1 |
| 4 |
| p |
| 2 |
∴|PQ|2=(2|PH|)2=4[(a-
| p |
| 2 |
令a-
| p |
| 2 |
| p |
| 2 |
故满足条件的直线l存在,其方程为y=
| p |
| 2 |
即抛物线的通径所在的直线.
解法2:(Ⅰ)前同解法1,再由弦长公式得|AB|=
| 1+k2 |
| 1+k2 |
| (x1+x2)2-4x1x2 |
| 1+k2 |
| 4p2k2+8p2 |
| 1+k2 |
| k2+2 |
又由点到直线的距离公式得d=
| 2p | ||
|
从而S△ABN=
| 1 |
| 2 |
| 1 |
| 2 |
| 1+k2 |
| k2+2 |
| 2p | ||
|
| k2+2 |
| 2 |
(Ⅱ)假设满足条件的直线l存在,其方程为y=a,则以AC为直径的圆的方程为(x-0)(x-x1)+(y-p)(y-y1)=0,
将直线方程y=a代入得x2-x1x+(a-p)(a-y1)=0,
则|x1-x2|2=
| x | 2 1 |
| p |
| 2 |
设直线l与以AC为直径的圆的交点为P(x3,y3),Q(x4,y4),
则有|PQ|=|x3-x4|=
4[(a-
|
(a-
|
令a-
| p |
| 2 |
| p |
| 2 |
| p |
| 2 |
即抛物线的通径所在的直线.
点评:本小题主要考查直线、圆和抛物线等平面解析几何的基础知识,考查综合运用数学知识进行推理运算的能力和解决问题的能力.

练习册系列答案
相关题目
 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是