题目内容
(1)已知集合 ,函数f(x)=log2(ax2-2x+2)的定义域为Q.若
,函数f(x)=log2(ax2-2x+2)的定义域为Q.若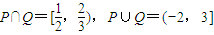 ,求实数a的值;
,求实数a的值;(2)函数f(x)定义在R上且f(x+3)=f(x),当
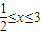 时,f(x)=log2(ax2-2x+2).若f(35)=1,求实数a的值.
时,f(x)=log2(ax2-2x+2).若f(35)=1,求实数a的值.
【答案】分析:(1)由条件知 ,ax2-2x+2>0解集
,ax2-2x+2>0解集 .由此能求出实数a的值.
.由此能求出实数a的值.
(2)由f(x)的周期为3,知f(35)=f(2),由此能求出a.
解答:解:(1)由条件知 ,
,
即ax2-2x+2>0解集 .
.
∴a<0且ax2-2x+2=0的二根为 .
.
∴ ,
,
∴ .
.
(2)∵f(x)的周期为3,
f(35)=f(3×11+2)
=f(2)
=log2(a•22-4+2)
=1,
所以a=1.
点评:本题考查集合的混合运算和函数周期性的求法,解题时要认真审题,注意函数性质的灵活运用.
 ,ax2-2x+2>0解集
,ax2-2x+2>0解集 .由此能求出实数a的值.
.由此能求出实数a的值.(2)由f(x)的周期为3,知f(35)=f(2),由此能求出a.
解答:解:(1)由条件知
 ,
,即ax2-2x+2>0解集
 .
.∴a<0且ax2-2x+2=0的二根为
 .
.∴
 ,
,∴
 .
.(2)∵f(x)的周期为3,
f(35)=f(3×11+2)
=f(2)
=log2(a•22-4+2)
=1,
所以a=1.
点评:本题考查集合的混合运算和函数周期性的求法,解题时要认真审题,注意函数性质的灵活运用.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
 ,函数
,函数 的定义域为Q,若P⊆Q,求实数a的取值范围;
的定义域为Q,若P⊆Q,求实数a的取值范围;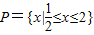 ,函数
,函数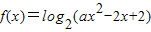 的定义域为Q,若P⊆Q,求实数a的取值范围;
的定义域为Q,若P⊆Q,求实数a的取值范围; ,函数
,函数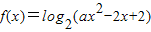 的定义域为Q,若P∩Q≠∅,求实数a的取值范围.
的定义域为Q,若P∩Q≠∅,求实数a的取值范围. ,函数f(x)=log2(ax2-2x+2)的定义域为Q.若
,函数f(x)=log2(ax2-2x+2)的定义域为Q.若 ,求实数a的值;
,求实数a的值; 时,f(x)=log2(ax2-2x+2).若f(35)=1,求实数a的值.
时,f(x)=log2(ax2-2x+2).若f(35)=1,求实数a的值.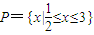 ,函数f(x)=log2(ax2-2x+2)的定义域为Q.若
,函数f(x)=log2(ax2-2x+2)的定义域为Q.若 ,求实数a的值;
,求实数a的值;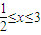 时,f(x)=log2(ax2-2x+2).若f(35)=1,求实数a的值.
时,f(x)=log2(ax2-2x+2).若f(35)=1,求实数a的值.