题目内容
已知集合A={x|x<-1或x>2},函数g(x)= 的定义域为集合B.
的定义域为集合B.
(Ⅰ)求A∩B和A∪B;
(Ⅱ)若C={x|4x+p<0},C⊆A,求实数p的取值范围.
解:(Ⅰ)依题意,得 B={ x|9-x2≥0}={ x|-3≤x≤3}-------
又∵集合A={x|x<-1或x>2},
∴A∩B=}={ x|-3≤x<-1,或2<x≤3},A∪B=R------
(Ⅱ)由4x+p<0得x<-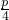
若C⊆A
则-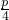 ≤-1-----
≤-1-----
得p≥4
∴实数p的取值范围是[4,+∞)-----
分析:(I)根据偶次被开方数必须大于等于0,可以求出集合B,根据已知中的集合A,结合集合交集和并集的定义,可得答案;
(II)由C中元素满足的性质4x+p<0,可得x<-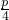 ,结合集合A={x|x<-1或x>2},及C⊆A,结合子集的定义,可得P的取值范围.
,结合集合A={x|x<-1或x>2},及C⊆A,结合子集的定义,可得P的取值范围.
点评:本题考查的知识点是函数的定义域,集合包含关系中的参数取值问题,集合的交集及并集运算,其中(1)的关键是求出集合B,(2)的关键是根据集合包含关系的定义构造关于p的不等式.
又∵集合A={x|x<-1或x>2},
∴A∩B=}={ x|-3≤x<-1,或2<x≤3},A∪B=R------
(Ⅱ)由4x+p<0得x<-
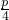
若C⊆A
则-
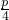 ≤-1-----
≤-1-----得p≥4
∴实数p的取值范围是[4,+∞)-----
分析:(I)根据偶次被开方数必须大于等于0,可以求出集合B,根据已知中的集合A,结合集合交集和并集的定义,可得答案;
(II)由C中元素满足的性质4x+p<0,可得x<-
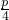 ,结合集合A={x|x<-1或x>2},及C⊆A,结合子集的定义,可得P的取值范围.
,结合集合A={x|x<-1或x>2},及C⊆A,结合子集的定义,可得P的取值范围.点评:本题考查的知识点是函数的定义域,集合包含关系中的参数取值问题,集合的交集及并集运算,其中(1)的关键是求出集合B,(2)的关键是根据集合包含关系的定义构造关于p的不等式.

练习册系列答案
相关题目