已知函数 (1)若函数y=在[1,2]内是减函数.求实数的取值范围 (2)令.是否存在实数,当时.函数的最小值为3.若存在求出值;若不存在.说明理由. 题目和参考答案——青夏教育精英家教网—

题目内容

已知函数

(1)若函数y=在[1,2]内是减函数，求实数的取值范围

（2）令，是否存在实数,当（e是自然对数的底数）时，函数的最小值为3，若存在求出值;若不存在，说明理由。

（1）

令h(x)= ,则h(1) ≤0且h(2) ≤0

得……………………………………6分

（2）假设存在a使得g(x)=ax-lnx,有最小值3

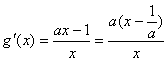
① 当a≤0时，＜0，g(x)在[0，e]上是单调递减

g_min(x)=g(e)=ae-1=3,a=(舍去)

② 当0<<e时，g(x)在(0，]上是单调递减，g(x)在(， e]上是单调递增

g_min(x)=g()=1+lna=3,a=(满足题意)

③ 当≥e时≤0，g(x)在(0，e]上是单调递减

g_min(x)=g(e)=ae-1=3,a=(舍去)

综上:存在a=使得当时,函数的最小值为3……………………12分

练习册系列答案

相关题目

(a＞0，a≠1)是奇函数，定义域为区间D（使表达式有意义的实数x 的集合）．
（1）求实数m的值，并写出区间D；
（2）若底数a＞1，试判断函数y=f（x）在定义域D内的单调性，并说明理由；
（3）当x∈A=[a，b）（A⊆D，a是底数）时，函数值组成的集合为[1，+∞），求实数a、b的值．

已知函数f（x）=px-

-2lnx、
（Ⅰ）若p=3，求曲f9想）在点（1，f（1））处的切线方程；
（Ⅱ）若p＞0且函f（x）在其定义域内为增函数，求实数p的取值范围；
（Ⅲ）若函数y=f（x）在x∈（0，3）存在极值，求实数p的取值范围．

已知函数f（x）=ax³+bx+c为R上的奇函数，且当x=1时，有极小值-1；函g(x)=-

x3+

x+t-

(t∈R，t≠0)
（1）求函数f（x）的解析式；
（2）若对于任意x∈[-2，2]，恒有f（x）＞g（x），求t的取值范围．

已知函数f(x)=

x2-3x-

．定义函数f（x）与实数m的一种符号运算为m?f（x）=f（x）•[f（x+m）-f（x）]．
（1）求使函数值f（x）大于0的x的取值范围；
（2）若g(x)=4?f(x)+

x2，求g（x）在区间[0，4]上的最大值与最小值；
（3）是否存在一个数列{a_n}，使得其前n项和Sn=4?f(n)+

n2．若存在，求出其通项；若不存在，请说明理由．

已知函数f（x）=log_ax（a＞0，且a≠1）自变量与函数值的部分对应值如下表：

x	2	1	0.25
f（x）	-1	0	2

则a=

；若函数g（x）=xf（x），则满足条件g（x）＞0的x的集合为

{x|0＜x＜1}

．

试题分类