题目内容
若函数 f（x）=Asin（x+?）（A＞0）在
处取最大值，则
- A.
一定是奇函数 - B.
一定是偶函数 - C.
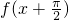一定是奇函数 - D.
一定是偶函数
D
分析：依题意，可求得φ=2kπ+
，k∈Z，代入f（x）的解析式，可对A，B，C，D作出判断．．
解答：∵函数 f（x）=Asin（x+?）（A＞0）在x=处取最大值，
∴+?=2kπ+
，k∈Z，
∴?=2kπ+，k∈Z，
∴f（x）=Asin（x+2kπ+）=Asin（x+），
∴f（x-）=Asin（x-）非奇非偶可排除A，同理可排除C，
∴f（x-）=Asinx，为奇函数，排除B；
f（x+）=Asin[（x+）+]=Acosx，为偶函数，D正确．
故选D．
点评：本题考查由y=Asin（ωx+φ）的部分图象确定其解析式，考查函数的奇偶性，属于中档题．
分析：依题意，可求得φ=2kπ+
，k∈Z，代入f（x）的解析式，可对A，B，C，D作出判断．．解答：∵函数 f（x）=Asin（x+?）（A＞0）在x=
处取最大值，∴
+?=2kπ+，k∈Z，∴?=2kπ+
，k∈Z，∴f（x）=Asin（x+2kπ+
）=Asin（x+），∴f（x-
）=Asin（x-）非奇非偶可排除A，同理可排除C，∴f（x-
）=Asinx，为奇函数，排除B；f（x+
）=Asin[（x+）+]=Acosx，为偶函数，D正确．故选D．
点评：本题考查由y=Asin（ωx+φ）的部分图象确定其解析式，考查函数的奇偶性，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
（2013•东至县一模）若函数f（x）=a（x+1）p（x-1）q（a＞0）在区间[-2，1]上的图象如图所示，则p，q的值可能是（ ）已知向量
=（-x，1），
=（x，tx），若函数f（x）=
•
在区间[-1，1]上不是单调函数，则实数t的取值范围是（ ）
| a |
| b |
| a |
| b |
| A、（-∞，-2]∪[2，+∞） |
| B、（-∞，-2）∪（2，+∞） |
| C、（-2，2） |
| D、[-2，2] |