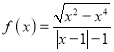题目内容
【题目】设函数![]() (实数
(实数![]() 为常数)
为常数)
(1)当![]() 时,证明
时,证明![]() 在
在![]() 上单调递减;
上单调递减;
(2)若![]() ,且
,且![]() 为偶函数,求实数
为偶函数,求实数![]() 的值;
的值;
(3)小金同学在求解函数![]() 的对称中心时,发现函数
的对称中心时,发现函数![]() 是一个复合函数,设
是一个复合函数,设![]() ,
,![]() ,则
,则![]() ,显然
,显然![]() 有对称中心,设为
有对称中心,设为![]() ,
,![]() 有反函数
有反函数![]() ,则
,则![]() 的对称中心为
的对称中心为![]() ,请问小金的做法是否正确?如果正确,请给出证明,并直接写出当
,请问小金的做法是否正确?如果正确,请给出证明,并直接写出当![]() 时
时![]() 的对称中心;如果错误,请举出反例,并用正确的方法直接写出当
的对称中心;如果错误,请举出反例,并用正确的方法直接写出当![]() 时
时![]() 的对称中心.
的对称中心.
【答案】(1)证明见解析;(2)![]() ;(3)若
;(3)若![]() ,
,![]() 的对称中心为
的对称中心为![]()
![]() ;若
;若![]() ,
,![]() 的对称中心为
的对称中心为![]() .
.
【解析】
(1)先将![]() 化简,再利用定义法证明单调性即可;
化简,再利用定义法证明单调性即可;
(2)由偶函数的性质![]() 化简求解即可得到a;
化简求解即可得到a;
(3)利用(1)作为反例可知小金的做法是错误的,分别讨论![]() 和
和![]() 的情况,结合对称点的性质
的情况,结合对称点的性质![]() 可得
可得![]() .
.
(1)当![]() 时,
时,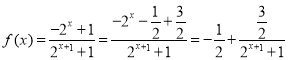 ,
,
任取![]() ,且
,且![]() ,
,
则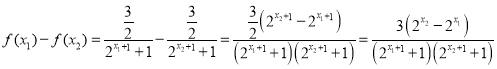 ,
,
由![]() 得,
得,![]() ,即
,即![]() ,又
,又![]() ,
,
所以![]() ,即
,即![]() ,故
,故![]() 在
在![]() 上单调递减;
上单调递减;
(2)依题意,![]() ,由
,由![]() 可得,
可得,![]() ,
,
整理可得,![]() ,解得
,解得![]() ;
;
(3)错误,令![]() ,则
,则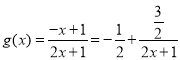 ,
,
显然![]() 有对称中心
有对称中心![]() ,
,![]() ,
,
很明显,![]() 没有意义,
没有意义,
当![]() 时,
时,![]() ,
,
若![]() ,
,![]() ,则直线上每一个点
,则直线上每一个点![]()
![]() 都是
都是![]() 的对称中心.
的对称中心.
若![]() ,设
,设![]() 的对称中心为
的对称中心为![]() ,
,
则![]() ,由此可得,
,由此可得,![]() ,
,![]() ,
,
即![]() 的对称中心为
的对称中心为![]() .
.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目