题目内容
(2013•盐城二模)(选修4-4:坐标系与参数方程)
已知圆C的参数方程为
(θ为参数),以原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为ρsinθ+ρcosθ=1,求直线l截圆C所得的弦长.
已知圆C的参数方程为
|
分析:通过平方关系式化圆的参数方程为普通方程,化极坐标分为直角坐标方程,利用圆心到直线的距离,半径,半弦长满足勾股定理,求出半弦长,然后求出弦长即可.
解答:解:圆C的参数方程为
(θ为参数),
所以圆C的方程为 x2+(y-2)2=1;圆的圆心坐标(0,2),半径为1,
直线l的极坐标方程为ρsinθ+ρcosθ=1,
所以直线l的方程为 x+y=1.
圆心到直线的距离为:d=
=
,
圆心到直线的距离,半径,半弦长满足勾股定理,
故所求弦长为2×
=
.…(10分)
|
所以圆C的方程为 x2+(y-2)2=1;圆的圆心坐标(0,2),半径为1,
直线l的极坐标方程为ρsinθ+ρcosθ=1,
所以直线l的方程为 x+y=1.
圆心到直线的距离为:d=
| |0+2-1| | ||
|
| ||
| 2 |
圆心到直线的距离,半径,半弦长满足勾股定理,
故所求弦长为2×
12-(
|
| 2 |
点评:本题考查圆的参数方程与直线的极坐标方程与普通方程的互化,直线与圆的位置关系的应用,考查计算能力.

练习册系列答案
相关题目
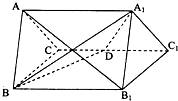 (2013•盐城二模)正三棱柱ABC-A1B1C1的所有棱长都为4,D为的CC1中点.
(2013•盐城二模)正三棱柱ABC-A1B1C1的所有棱长都为4,D为的CC1中点.