题目内容
已知函数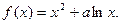
（1）当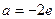
时，求函数
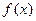的单调区间和极值。
（2）若函数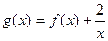
在[1，4]上是减函数，求实数
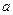的取值范围.
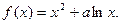
（1）当
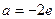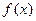时，求函数的单调区间和极值。（2）若函数
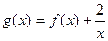在[1，4]上是减函数，求实数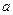的取值范围.（1）减区间是
；增区间是
；极小值是
（2）
；增区间是；极小值是（2）
（1）函数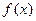的定义域为（0，+∞）。
当
时，
当
变化时，
的变化情况如下：
的单调递减区间是 ；单调递增区间是。
极小值是 6分
（2）由
，得
又函数
为[1，4]上的单调减函数。
则
在[1，4]上恒成立，
所以不等式
在[1，4]上恒成立，
即
在[1，4]上恒成立。 设
，显然
在[1，4]上为减函数，所以的最小值为
的取值范围是
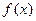的定义域为（0，+∞）。当
时， 当变化时，的变化情况如下：的单调递减区间是 ；单调递增区间是。极小值是
6分（2）由
，得又函数
为[1，4]上的单调减函数。则
在[1，4]上恒成立，所以不等式
在[1，4]上恒成立，即
在[1，4]上恒成立。 设，显然在[1，4]上为减函数，所以的最小值为的取值范围是 
练习册系列答案
世纪百通期末金卷系列答案
相关题目
.
时，求函数
在
上的值域；
，若存在
，使得以
为三边长的三角形不存在，求实数
的取值范围.
的定义域是（ ）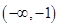
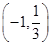
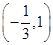
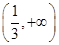
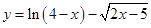, 则此函数的定义域为 ．
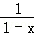+lg（1+x）的定义域是（ ）
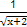的定义域是( )
在其定义域内的一个子区间
内不是单调函数，则实数k的取值范围( )
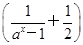x3(a>0且a≠1)．
的值域相同的函数为（ ）
