题目内容
已知在△ABC中,∠A,∠B,∠C所对的边分别为a,b,c,若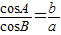 且sinC=cosA
且sinC=cosA(Ⅰ)求角A、B、C的大小;
(Ⅱ)设函数
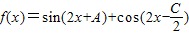 ,求函数f(x)的单调递增区间,并指出它相邻两对称轴间的距离.
,求函数f(x)的单调递增区间,并指出它相邻两对称轴间的距离.
【答案】分析:(Ⅰ)根据正弦定理求得sin2A和sin2B的关系进而得出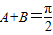 .进而根据sinC=cosA求得A,B,C.
.进而根据sinC=cosA求得A,B,C.
(Ⅱ)把(Ⅰ)中的A,B,C代入f(x)整理后根据正弦函数的性质可得函数f(x)的单调区间.
解答:解:(Ⅰ)由题设及正弦定理知: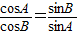 ,得sin2A=sin2B
,得sin2A=sin2B
∴2A=2B或2A+2B=π,即A=B或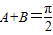
当A=B时,有sin(π-2A)=cosA,即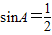 ,得
,得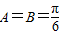 ,
,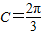 ;
;
当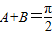 时,有
时,有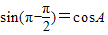 ,即cosA=1不符题设
,即cosA=1不符题设
∴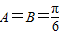 ,
,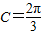
(Ⅱ)由(Ⅰ)及题设知: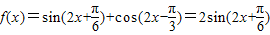
当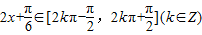 时,
时,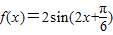 为增函数
为增函数
即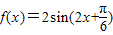 的单调递增区间为
的单调递增区间为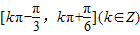 .
.
它的相邻两对称轴间的距离为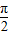 .
.
点评:本题主要考查正弦定理在解三角形中的应用.解决本题的关键是,利用正弦定理把三角形边角问题转化为三角函数问题是解题的关键,三角形与三角函数、向量与三角函数高考考查的热点.
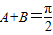 .进而根据sinC=cosA求得A,B,C.
.进而根据sinC=cosA求得A,B,C.(Ⅱ)把(Ⅰ)中的A,B,C代入f(x)整理后根据正弦函数的性质可得函数f(x)的单调区间.
解答:解:(Ⅰ)由题设及正弦定理知:
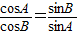 ,得sin2A=sin2B
,得sin2A=sin2B∴2A=2B或2A+2B=π,即A=B或
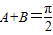
当A=B时,有sin(π-2A)=cosA,即
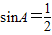 ,得
,得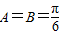 ,
,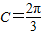 ;
;当
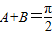 时,有
时,有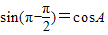 ,即cosA=1不符题设
,即cosA=1不符题设∴
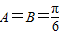 ,
,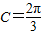
(Ⅱ)由(Ⅰ)及题设知:
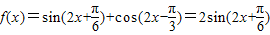
当
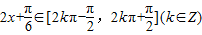 时,
时,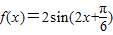 为增函数
为增函数即
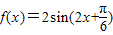 的单调递增区间为
的单调递增区间为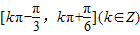 .
.它的相邻两对称轴间的距离为
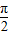 .
.点评:本题主要考查正弦定理在解三角形中的应用.解决本题的关键是,利用正弦定理把三角形边角问题转化为三角函数问题是解题的关键,三角形与三角函数、向量与三角函数高考考查的热点.

练习册系列答案
相关题目