题目内容
已知函数
(1)若 在[-3,2]上具有单调性,求实数
在[-3,2]上具有单调性,求实数 的取值范围。
的取值范围。
(2)若 的
的 有最小值为-12,求实数
有最小值为-12,求实数 的值;
的值;
(1)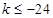 或
或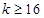 ;(2)
;(2)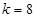 或
或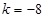
解析试题分析:(1)二次函数的单调性与对称轴有关,单调区间在对称轴的一侧,可数形结合解题;  图像开口上, 对称轴为
图像开口上, 对称轴为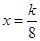 ,区间
,区间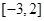 在对称轴左侧
在对称轴左侧 为单调减函数, 区间
为单调减函数, 区间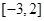 在对称轴右侧
在对称轴右侧 为单调增函数,
为单调增函数,
(2)二次函数在区间上的最值在端点处或顶点处,遇到对称轴或区间含有待定的字母,则要按对称轴在不在区间内以及区间中点进行讨论.  图像开口上,当对称轴为
图像开口上,当对称轴为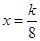 在区间
在区间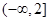 内时,最小值位于对称轴处; 当区间
内时,最小值位于对称轴处; 当区间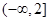 在对称轴左侧
在对称轴左侧 为单调减函数,最小值位于右端点处.
为单调减函数,最小值位于右端点处.
试题解析:
(1)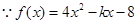 的对称轴为
的对称轴为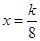
又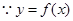 在
在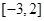 上具有单调性
上具有单调性
所以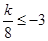 或
或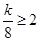
即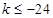 或
或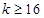
(2) 由 在
在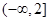 有最小值为
有最小值为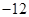
Ⅰ.当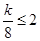 即
即 时
时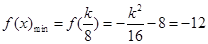
解得: 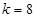 或
或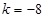
Ⅱ.当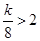 即
即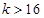 时
时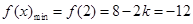
解得: 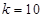 (舍)
(舍)
综上所述: 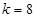 或
或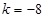
考点:二次函数单调性与最值.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 ,若存在实数对(
,若存在实数对( ),使得等式
),使得等式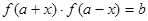 对定义域中的每一个
对定义域中的每一个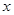 都成立,则称函数
都成立,则称函数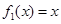 是否为 “(
是否为 “(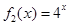 是“(
是“(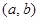 ;,
;, 是“(
是“(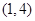 .当
.当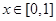 时,
时,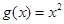
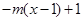
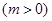 ,若当
,若当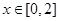 时,都有
时,都有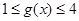 ,试求
,试求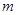 的取值范围.
的取值范围.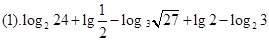
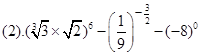
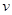 (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度 (单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过40辆/千米时,车流速度为80千米/小时.研究表明:当
(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过40辆/千米时,车流速度为80千米/小时.研究表明:当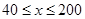 时,车流速度
时,车流速度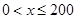 时,求函数
时,求函数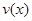 的表达式;
的表达式;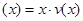 ,
,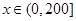 可以达到最大,并求出最大值.
可以达到最大,并求出最大值. 和分别以
和分别以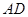 、
、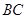 为直径的两个半圆组成,塑胶跑道宽8米,已知塑胶跑道每平方米造价为150元,其它部分造价每平方米80元,
为直径的两个半圆组成,塑胶跑道宽8米,已知塑胶跑道每平方米造价为150元,其它部分造价每平方米80元,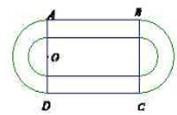
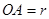 (米),写出塑胶跑道面积
(米),写出塑胶跑道面积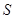 与
与 的函数关系式
的函数关系式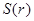 ;
;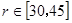 ,问当
,问当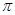 取3近似计算).
取3近似计算).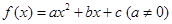 满足
满足 ,对任意
,对任意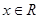 都有
都有 ,且
,且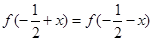 .
. 的解析式;
的解析式;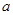 ,使函数
,使函数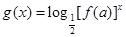 在
在 上为减函数?若存在,求出实数
上为减函数?若存在,求出实数 (m∈N+)的图象关于y轴对称,且在(0,+∞)上是减函数,求满足
(m∈N+)的图象关于y轴对称,且在(0,+∞)上是减函数,求满足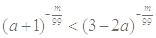 的a的取值范围.
的a的取值范围. ,
, ,其中实数
,其中实数 .
. ,求函数
,求函数 的单调区间;
的单调区间; 与
与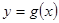 的图象只有一个公共点且
的图象只有一个公共点且 存在最小值时,记
存在最小值时,记 ,求
,求 内均为增函数,求实数
内均为增函数,求实数 的取值范围.
的取值范围.