题目内容
【题目】函数![]() .
.
(1)若函数![]() 的图象在
的图象在![]() 处的切线过
处的切线过![]() ,求
,求![]() 的值;
的值;
(2)![]() 在
在![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)1;(2)![]() .
.
【解析】
(1)先对函数求导,得到![]() ,根据题意,得到
,根据题意,得到![]() ,推出
,推出![]() ,设
,设![]() ,
,![]() ,对其求导,研究其单调性,求出最小值,即可得出结果;
,对其求导,研究其单调性,求出最小值,即可得出结果;
(2)先由题意,将![]() 在
在![]() 恒成立,转化为
恒成立,转化为![]() 在
在![]() 恒成立,设
恒成立,设![]() ,
,![]() ,对其求导,分
,对其求导,分![]() ,
,![]() ,
,![]() 三种情况讨论,研究其单调性,得到其大致范围,即可得出结果.
三种情况讨论,研究其单调性,得到其大致范围,即可得出结果.
(1)因为![]() ,所以
,所以![]() ,
,
由于在![]() 处的切线过
处的切线过![]() ,
,
所以![]() ,即
,即![]() ,
,
化简得![]() ,即
,即![]() ,
,
设![]() ,
,![]() ,则
,则![]() ,
,
由![]() 得
得![]() ;由
;由![]() 得
得![]() ;
;
从而![]() 在
在![]() 单调递增,再
单调递增,再![]() 单调递减;因此
单调递减;因此![]() ,
,
所以![]() 有唯一根
有唯一根![]() ;
;
(2)由![]() 得
得![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
因此,![]() 在
在![]() 恒成立,即是
恒成立,即是![]() 在
在![]() 恒成立;
恒成立;
设![]() ,
,![]() ,
,
则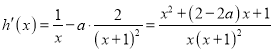 ,
,
当![]() 时,
时,![]() ,此时
,此时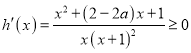 恒成立,
恒成立,
所以![]() 单增,因此
单增,因此![]() ,满足题意;
,满足题意;
当![]() 时,
时,![]() 显然恒成立,此时
显然恒成立,此时![]() 单增,
单增,
所以![]() ,也满足题意;
,也满足题意;
当![]() 时,由
时,由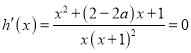 得
得![]() ,
,![]() ,
,
所以方程![]() 必有两不等实根,不妨设为
必有两不等实根,不妨设为![]() ,
,
由根与系数关系,![]() ,所以方程
,所以方程![]() 在
在![]() 有唯一根
有唯一根![]() ,
,
即![]() 在
在![]() 有唯一根
有唯一根![]() ,所以易得:
,所以易得:![]() 在
在![]() 单减,
单减,![]() 单增,
单增,
则![]() ,与题意矛盾,不成立;
,与题意矛盾,不成立;
综上,![]() .
.

【题目】若A1,A2,…,Am为集合A={1,2,…,n}(n≥2且n∈N*)的子集,且满足两个条件:
①A1∪A2∪…∪Am=A;
②对任意的{x,y}A,至少存在一个i∈{1,2,3,…,m},使Ai∩{x,y}={x}或{y}.则称集合组A1,A2,…,Am具有性质P.
如图,作n行m列数表,定义数表中的第k行第l列的数为akl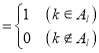 .
.
a11 | a12 | … | a1m |
a21 | a22 | … | a2m |
… | … | … | … |
an1 | an2 | … | anm |
(1)当n=4时,判断下列两个集合组是否具有性质P,如果是请画出所对应的表格,如果不是请说明理由;
集合组1:A1={1,3},A2={2,3},A3={4};
集合组2:A1={2,3,4},A2={2,3},A3={1,4}.
(2)当n=7时,若集合组A1,A2,A3具有性质P,请先画出所对应的7行3列的一个数表,再依此表格分别写出集合A1,A2,A3;
(3)当n=100时,集合组A1,A2,…,At是具有性质P且所含集合个数最小的集合组,求t的值及|A1|+|A2|+…|At|的最小值.(其中|Ai|表示集合Ai所含元素的个数)