题目内容

如图，已知F1、F2是椭圆（）的左、右焦点，点P在椭圆C上，线段PF2与圆相切于点Q，且点Q为线段PF2的中点，则椭圆C的离心率为_______．

 

【答案】

【解析】解：连接OQ，F1P如下图所示：

则由切线的性质，则OQ⊥PF2，

又由点Q为线段PF2的中点，O为F1F2的中点

∴OQ∥F1P

∴PF2⊥PF1，

∴ PF1 • PF2 =0

故|PF2|=2a-2b，

且| PF1|=2b，| F1F2|=2c，

则|F1F2|2=| PF1|2+| F1F2|2

得4c2=4b2+4（a2-2ab+b2）

解得：b=2/ 3 a

则c=  a

故椭圆的离心率为： 故答案为：0，  ．

 

练习册系列答案
相关题目
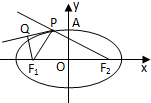精英家教网如图，已知F1、F2是椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的左、右焦点，点P在椭圆C上，线段PF2与圆x2+y2=b2相切于点Q，且点Q为线段PF2的中点，则
PF1
•
PF2
=
 
；椭圆C的离心率为
 
．
精英家教网如图，已知F1，F2是椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的左、右焦点，点P在椭圆C上，线段PF2与圆x2+y2=b2相切于点Q，且点Q为线段PF2的中点，则椭圆C的离心率为
 
．
（2012•鹰潭一模）如图，已知F1，F2是椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的左、右焦点，点P在椭圆C上，线段PF2与圆x2+y2=b2相切于点Q，且点Q为线段PF2的中点，则椭圆C的离心率为（　　）
如图，已知F1、F2分别为椭圆C1：
y2
a2
+
x2
b2
=1(a＞b＞0)的上、下焦点，其中F1也是抛物线C2：x2=4y的焦点，点M是C1与C2在第二象限的交点，且|MF1|=
5
3
．
（1）求椭圆C1的方程；
（2）已知点P（1，3）和圆O：x2+y2=b2，过点P的动直线l与圆O相交于不同的两点A，B，在线段AB上取一点Q，满足：
AP
=-λ
PB
，
AQ
=λ
QB
（λ≠0且λ≠±1），
求证：点Q总在某条定直线上．
精英家教网如图，已知F1、F2是椭圆
x2
172
+
y2
152
=1的左、右焦点，A是椭圆短轴的一个端点，P是椭圆上任意一点，过F1引∠F1PF2的外角平分线的垂线，垂足为Q，则|AQ|的最大值为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网