题目内容
设向量a=(cosα,sinα),b=(cosβ,sinβ),其中0<α<β<π,若|2a+b|=|a-2b|,则β-α=( )
A.![]() B.-
B.-![]()
C.![]() D.-
D.-![]()
解析:由|2a+b|=|a-2b|得3|a|2-3|b|2+8a·b=0,
而|a|=|b|=1,故a·b=0,
∴cosαcosβ+sinαsinβ=0,
即cos(α-β)=0,由于0<α<β<π,
故-π<α-β<0,∴α-β=-![]() ,即β-α=
,即β-α=![]() .
.
答案:A

练习册系列答案
相关题目
 ,cos
,cos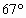 ),b=(cos
),b=(cos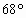 ,cos
,cos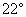 ),c=a+tb(t∈R)
),c=a+tb(t∈R)