题目内容
定义域为R的函数 ,若关于x的函数
,若关于x的函数 有5个不同的零点x1,x2,x3,x4,x5,则x12+x22+x32+x42+x52等于
有5个不同的零点x1,x2,x3,x4,x5,则x12+x22+x32+x42+x52等于
- A.

- B.16
- C.5
- D.15
D
分析:作出f(x)的图象,由图知,只有当f(x)=1时有两解,欲使关于x的方程 有5个不同的实数解x1,x2,x3,x4,x5,则必有f(x)=1这个等式,由根与系数的关系得另一个根是f(x)=-1,从而得x=0.故可得5个根的平方和,问题得到解决.
有5个不同的实数解x1,x2,x3,x4,x5,则必有f(x)=1这个等式,由根与系数的关系得另一个根是f(x)=-1,从而得x=0.故可得5个根的平方和,问题得到解决.
解答:作出f(x)的图象:
由图知,只有当f(x)=1时有两解;
∵关于x的方程f2(x)+bf(x)-1=0有5个不同的实数解:
x1,x2,x3,x4,x5,
∴必有f(x)=1,从而x1=1,x2=2.
由根与系数的关系得另一个根是f(x)=-1,从而得x3=0.
∴原方程的五个根分别为:-1,0,1,2,3,
故可得x12+x22+x32+x42+x52=15.
故选D.
点评:本题考查复合函数的零点问题,复合函数的零点的问题,必须要将f(x)看成整体,利用整体思想解决.数形结合也是解决此题的关键,利用函数的图象可以加强直观性,同时也便于问题的理解.
分析:作出f(x)的图象,由图知,只有当f(x)=1时有两解,欲使关于x的方程
 有5个不同的实数解x1,x2,x3,x4,x5,则必有f(x)=1这个等式,由根与系数的关系得另一个根是f(x)=-1,从而得x=0.故可得5个根的平方和,问题得到解决.
有5个不同的实数解x1,x2,x3,x4,x5,则必有f(x)=1这个等式,由根与系数的关系得另一个根是f(x)=-1,从而得x=0.故可得5个根的平方和,问题得到解决.解答:作出f(x)的图象:

由图知,只有当f(x)=1时有两解;
∵关于x的方程f2(x)+bf(x)-1=0有5个不同的实数解:
x1,x2,x3,x4,x5,
∴必有f(x)=1,从而x1=1,x2=2.
由根与系数的关系得另一个根是f(x)=-1,从而得x3=0.
∴原方程的五个根分别为:-1,0,1,2,3,
故可得x12+x22+x32+x42+x52=15.
故选D.
点评:本题考查复合函数的零点问题,复合函数的零点的问题,必须要将f(x)看成整体,利用整体思想解决.数形结合也是解决此题的关键,利用函数的图象可以加强直观性,同时也便于问题的理解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,若关于x的方程f2(x)+bf(x)+c=0有3个不同的整数解x1,x2,x3,则x12+x22+x32等于 .
,若关于x的方程f2(x)+bf(x)+c=0有3个不同的整数解x1,x2,x3,则x12+x22+x32等于 . ,若关于x的方程f2(x)+bf(x)+c=0有3个不同的整数解x1,x2,x3,则x12+x22+x32等于 .
,若关于x的方程f2(x)+bf(x)+c=0有3个不同的整数解x1,x2,x3,则x12+x22+x32等于 . ,若关于
,若关于 的方程
的方程 有3个不同的实根,则关于x的不等式
有3个不同的实根,则关于x的不等式 的解集为( )
的解集为( ) D. (c,1)
D. (c,1) ,若关于
,若关于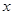 的方程
的方程 有3个不同的实根
有3个不同的实根 ,则
,则 等于
等于 C. 13 D.
C. 13 D. 