题目内容
已知( +x2
+x2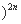 的展开式的二项式系数和比(3x-1)n的展开式的二项式系数和大992.
的展开式的二项式系数和比(3x-1)n的展开式的二项式系数和大992.
(1) 求 的展开式中二项式系数最大的项;
的展开式中二项式系数最大的项;
(2) 求 的展开式中系数的绝对值最大的项.
的展开式中系数的绝对值最大的项.
由题意知,22n-2n=992,即(2n-32)(2n+31)=0,
所以2n=32,解得n=5.
(1) 由二项式系数的性质知, 的展开式中第6项的二项式系数最大,
的展开式中第6项的二项式系数最大,
即T6= · (2x)5·
· (2x)5· =-8 064.
=-8 064.
(2) 因为Tr+1= ·(2x)10-r·
·(2x)10-r·
=(-1)r ·210-r·x10-2r,
·210-r·x10-2r,
设第r+1项的系数的绝对值最大,
所以
得 即
即
解得 ≤r≤
≤r≤ .因为r∈Z,所以r=3,
.因为r∈Z,所以r=3,
故系数的绝对值最大的项是第4项,T4=- ·27·x4=-15 360x4.
·27·x4=-15 360x4.

练习册系列答案
相关题目

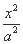 +
+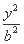 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为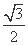 ,以原点为圆心、椭圆C的短半轴长为半径的圆与直线x-y+2=0相切.
,以原点为圆心、椭圆C的短半轴长为半径的圆与直线x-y+2=0相切.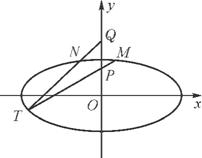
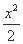 -
- =1的准线经过椭圆
=1的准线经过椭圆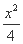 +
+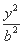 =1(b>0)的焦点,则b= .
=1(b>0)的焦点,则b= . B.输入、输出框
B.输入、输出框