题目内容
已知等差数列{an2}中,首项a12=1,公差d=1,an>0,n∈N*.
(1)求数列{an}的通项公式;
(2)设bn= ,求数列{bn}的前120项的和T120.
,求数列{bn}的前120项的和T120.
解:(1)∵{an2}是等差数列,等差d=1,首项a12=1,
∴an2=1+(n-1)×1=n,
又an>0,
∴an= ;
;
(2)∵bn= =
=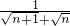 =
= -
- ,
,
∴T120=( -1+(
-1+( -
- )+…+(
)+…+( -
-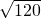 )=
)= -1=10.
-1=10.
分析:(1)由等差数列{an2}的首项a12和公差d,利用等差数列的通项公式求出{an2}的通项公式,然后根据an大于0,开方可得数列{an}的通项公式;
(2)把(1)求得{an}的通项公式代入bn= 中,分母有理化化简后即可得到数列{bn}的通项公式,然后列举出数列{bn}的前120项的和,抵消化简可得值.
中,分母有理化化简后即可得到数列{bn}的通项公式,然后列举出数列{bn}的前120项的和,抵消化简可得值.
点评:此题考查学生灵活运用等差数列的通项公式化简求值,会进行数列的求和运算,是一道中档题.
∴an2=1+(n-1)×1=n,
又an>0,
∴an=
 ;
;(2)∵bn=
 =
=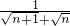 =
= -
- ,
,∴T120=(
 -1+(
-1+( -
- )+…+(
)+…+( -
-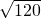 )=
)= -1=10.
-1=10.分析:(1)由等差数列{an2}的首项a12和公差d,利用等差数列的通项公式求出{an2}的通项公式,然后根据an大于0,开方可得数列{an}的通项公式;
(2)把(1)求得{an}的通项公式代入bn=
 中,分母有理化化简后即可得到数列{bn}的通项公式,然后列举出数列{bn}的前120项的和,抵消化简可得值.
中,分母有理化化简后即可得到数列{bn}的通项公式,然后列举出数列{bn}的前120项的和,抵消化简可得值.点评:此题考查学生灵活运用等差数列的通项公式化简求值,会进行数列的求和运算,是一道中档题.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
 12分)已知等差数列{an2
12分)已知等差数列{an2 }中,首项a12=1,公差d=1,an>0,n∈N
}中,首项a12=1,公差d=1,an>0,n∈N *.
*.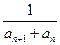 ,数列{bn}的前120项和T120;
,数列{bn}的前120项和T120;  ,数
,数 列{bn}的前n项和为Tn;
列{bn}的前n项和为Tn; 当n>3时,
当n>3时,  2
2
 ,数列{bn}的前n项和为Tn; ①求T120;
②求证:当n>3时, 2
,数列{bn}的前n项和为Tn; ①求T120;
②求证:当n>3时, 2