题目内容
(本小题满分12分)
设函数![]() ,
,![]() .
.
(Ⅰ)若![]() ,求
,求![]() 的极小值;
的极小值;
(Ⅱ)在(Ⅰ)的条件下,是否存在实常数![]() 和
和![]() ,使得
,使得![]() 和
和![]() ?若存在,求出
?若存在,求出![]() 和
和![]() 的值.若不存在,说明理由.
的值.若不存在,说明理由.
(Ⅲ)设![]() 有两个零点
有两个零点![]() ,且
,且![]() 成等差数列,
成等差数列,
试探究![]() 值的符号.
值的符号.
解:(1)由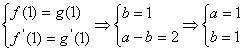
![]()
利用导数的方法求得![]() 的极小值为
的极小值为![]() …………………2分
…………………2分
(2)因为![]() 与
与![]() 有一个公共点(1,1),而函数
有一个公共点(1,1),而函数![]() 在点(1,1)的
在点(1,1)的
切线方程为![]() ,下面验证:
,下面验证:![]() 都成立即可。
都成立即可。
由于![]() ,知
,知![]() 恒成立;
恒成立;
设![]()
![]()
![]() 得
得![]()
在(0,1)上,![]() ,
,![]() 单调递增;
单调递增;
在 ![]() 上,
上,![]() ,
,![]() 单调递减;
单调递减;
又因为![]() 在
在![]() 处连续,所以
处连续,所以![]()
所以![]()
故存在这样的k和m,且k=2,m= -1。 ………………………………6分
(3)![]() 的符号为正,理由为:因为
的符号为正,理由为:因为![]() 有两个零点
有两个零点![]() ,则有
,则有 ,两式相减,得
,两式相减,得
![]()
(理科数学试卷答案 共5页—第3页)
即 ![]()
于是![]()
![]()
![]()
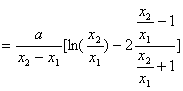
当![]() 时,令
时,令![]() ,则
,则![]() ,
,![]()
![]()
设![]() ,则
,则![]()
所以![]() 在
在![]() 上为单调增函数,而
上为单调增函数,而![]() ,所以
,所以![]() >0,
>0,
又因a>0, ![]() ,所以
,所以![]()
同理,当![]() 时,同理可得
时,同理可得![]()
综上所述![]() 的符号为正。 ……………………………12分
的符号为正。 ……………………………12分

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案
相关题目