题目内容
已知函数f(x)=ax3+bx2+cx(a≠0)定义在R上的奇函数,且x=-1时,函数取极值1.
(1)求a,b,c的值;
(2)若对任意的x1,x2∈[-1,1],均有|f(x1)-f(x2)|≤s成立,求s的最小值.
解:(1)∵f(x)=ax3+bx2+cx(a≠0)是定义R上的奇函数
∴b=0
∴f(x)=ax3+cx,∴f′(x)=3ax2+c
依题意有f′(-1)=0且f(-1)=1
即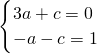 ,解得,a=
,解得,a= ,c=-
,c=-
∴f(x)= x3+-
x3+- x
x
(2) ,
,
x∈(-1,1)时f′(x)<0,
∴f(x)在x∈[-1,1]上是减函数,
即f(1)≤f(x)≤f(-1),
则|f(x)|≤1,?fmax(x)=1,fmin(x)=-1,
当x1,x2∈[-1,1]时,|f(x1)-f(x2)|≤|f(x)max|+|f(x)min|≤1+1=2
∴|f(x1)-f(x2)|≤s中s的最小值为2,
∴s的最小值2.
分析:(1)欲求f(x)的解析式,只需找到关于a,b,c的三个等式,求出a,b,c的值,根据函数的奇偶性可得到一个含a,b,c的等式,根据x=-1时,取得极值1,可知函数在x=-1时,导数等于0,且x=-1时,函数值等于1,又可得到两个含a,b,c的等式,三个等式联立,解出a,b,c即可.
(2)利用导数得到函数为减函数f(1)≤f(x)≤f(-1)得到|f(x)|≤1,从而得出f(x)的最大最小值,从而求出当|f(x1)-f(x2)|≤s成立时s的最小值.
点评:本题主要考查了利用导数求闭区间上函数的最值,考查学生利用导数研究函数极值的能力,以及绝对值不等式的性质.属于中档题.
∴b=0
∴f(x)=ax3+cx,∴f′(x)=3ax2+c
依题意有f′(-1)=0且f(-1)=1
即
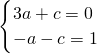 ,解得,a=
,解得,a= ,c=-
,c=-
∴f(x)=
 x3+-
x3+- x
x(2)
 ,
,x∈(-1,1)时f′(x)<0,
∴f(x)在x∈[-1,1]上是减函数,
即f(1)≤f(x)≤f(-1),
则|f(x)|≤1,?fmax(x)=1,fmin(x)=-1,
当x1,x2∈[-1,1]时,|f(x1)-f(x2)|≤|f(x)max|+|f(x)min|≤1+1=2
∴|f(x1)-f(x2)|≤s中s的最小值为2,
∴s的最小值2.
分析:(1)欲求f(x)的解析式,只需找到关于a,b,c的三个等式,求出a,b,c的值,根据函数的奇偶性可得到一个含a,b,c的等式,根据x=-1时,取得极值1,可知函数在x=-1时,导数等于0,且x=-1时,函数值等于1,又可得到两个含a,b,c的等式,三个等式联立,解出a,b,c即可.
(2)利用导数得到函数为减函数f(1)≤f(x)≤f(-1)得到|f(x)|≤1,从而得出f(x)的最大最小值,从而求出当|f(x1)-f(x2)|≤s成立时s的最小值.
点评:本题主要考查了利用导数求闭区间上函数的最值,考查学生利用导数研究函数极值的能力,以及绝对值不等式的性质.属于中档题.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目