题目内容
A.(极坐标系与参数方程选做题) 已知圆ρ=3cosθ,则圆截直线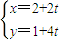 (t是参数)所得的弦长为 ;
(t是参数)所得的弦长为 ;B.(几何证明选讲选做题) 如图:PA与圆O相切于A,PCB为圆O的割线,并且不过圆心O,已知∠BPA=30°,
 ,PC=1,则圆O的半径等于 .
,PC=1,则圆O的半径等于 .
【答案】分析:A把极坐标方程和参数方程化为普通方程,直线经过圆心,可求出弦长
B连AO并延长,根据切线的性质定理得到Rt△PAD,根据切割线定理得到PA2=PC•PB,根据相交弦定理得到CD•DB=AD•DE,最后即可解得圆O的半径.
解答:解:A:圆ρ=3cosθ,它的直角坐标方程x2+y2-3x=0,圆心坐标( ,0),半径为
,0),半径为  ,直线
,直线  (t是参数)的直角坐标方程为:2x-y-3=0,直线经过圆心,所得的弦长为:3.
(t是参数)的直角坐标方程为:2x-y-3=0,直线经过圆心,所得的弦长为:3.
故答案为:3.
B :如图,连AO并延长,交圆O与另一点E,交割线PCB于点D,
:如图,连AO并延长,交圆O与另一点E,交割线PCB于点D,
则Rt△PAD中,由∠DPA=30°, ,得AD=2,PD=4,而PC=1,
,得AD=2,PD=4,而PC=1,
故CD=3,由切割线定理,得PA2=PC•PB,即 ,则PB=11,
,则PB=11,
故DB=8.
设圆O的半径为R,
由相交弦定理,CD•DB=AD•DE,即3×8=2(2R-2),
得R=7;
故答案为:7.
点评:A题考查直线与圆的位置关系,注意经过圆的直线弦长的求法;B本小题主要考查圆的切割线定理和相交弦定理.属于中档题
B连AO并延长,根据切线的性质定理得到Rt△PAD,根据切割线定理得到PA2=PC•PB,根据相交弦定理得到CD•DB=AD•DE,最后即可解得圆O的半径.
解答:解:A:圆ρ=3cosθ,它的直角坐标方程x2+y2-3x=0,圆心坐标(
 ,0),半径为
,0),半径为  ,直线
,直线  (t是参数)的直角坐标方程为:2x-y-3=0,直线经过圆心,所得的弦长为:3.
(t是参数)的直角坐标方程为:2x-y-3=0,直线经过圆心,所得的弦长为:3.故答案为:3.
B
 :如图,连AO并延长,交圆O与另一点E,交割线PCB于点D,
:如图,连AO并延长,交圆O与另一点E,交割线PCB于点D,则Rt△PAD中,由∠DPA=30°,
 ,得AD=2,PD=4,而PC=1,
,得AD=2,PD=4,而PC=1,故CD=3,由切割线定理,得PA2=PC•PB,即
 ,则PB=11,
,则PB=11,故DB=8.
设圆O的半径为R,
由相交弦定理,CD•DB=AD•DE,即3×8=2(2R-2),
得R=7;
故答案为:7.
点评:A题考查直线与圆的位置关系,注意经过圆的直线弦长的求法;B本小题主要考查圆的切割线定理和相交弦定理.属于中档题

练习册系列答案
相关题目
 (A)(不等式选讲)不等式log3(|x-4|+|x+5|)>a对于一切x∈R恒成立,则实数a的取值范围是
(A)(不等式选讲)不等式log3(|x-4|+|x+5|)>a对于一切x∈R恒成立,则实数a的取值范围是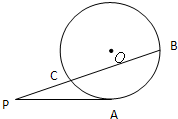 A.(极坐标系与参数方程选做题) 已知圆ρ=3cosθ,则圆截直线
A.(极坐标系与参数方程选做题) 已知圆ρ=3cosθ,则圆截直线 A.(极坐标系与参数方程选做题) 已知圆ρ=3cosθ,则圆截直线
A.(极坐标系与参数方程选做题) 已知圆ρ=3cosθ,则圆截直线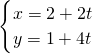 (t是参数)所得的弦长为________;
(t是参数)所得的弦长为________;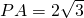 ,PC=1,则圆O的半径等于________.
,PC=1,则圆O的半径等于________.