题目内容
已知 ,
,
(1)求 和
和 的夹角;
的夹角;
(2)当m取何值时, 与
与 共线?
共线?
(3)当m取何值时, 与
与 垂直?
垂直?
解:(1)由 ,得
,得 ,
,
即7×1-6×4-11×1×2×cosθ=-6,解得 ,
,
∵0°≤θ≤180°,∴θ=120°
(2)∵ ∥
∥ ,∴令
,∴令 ,
,
即 ,∵
,∵ 不共线,
不共线,
∴ ,解得
,解得
(3)∵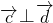 ,∴
,∴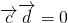 ,即
,即 ,
,
得 ,
,
即m2-21m+20=0,∴m=1或m=20
分析:(1)依照向量数量积的运算法则,将 化简整理,即可求出夹角.
化简整理,即可求出夹角.
(2)根据向量共线定理,存在λ使 ,再根据向量相等概念解出m即可.
,再根据向量相等概念解出m即可.
(3)若 与
与 垂直,则
垂直,则 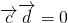 ,化成关于m的方程并解出m即可.
,化成关于m的方程并解出m即可.
点评:本题考查向量数量积、夹角的计算,向量共线、向量垂直的条件及判定.是向量中的基本知识,本题属于基础题.
 ,得
,得 ,
,即7×1-6×4-11×1×2×cosθ=-6,解得
 ,
,∵0°≤θ≤180°,∴θ=120°
(2)∵
 ∥
∥ ,∴令
,∴令 ,
,即
 ,∵
,∵ 不共线,
不共线,∴
 ,解得
,解得
(3)∵
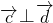 ,∴
,∴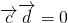 ,即
,即 ,
,得
 ,
,即m2-21m+20=0,∴m=1或m=20
分析:(1)依照向量数量积的运算法则,将
 化简整理,即可求出夹角.
化简整理,即可求出夹角.(2)根据向量共线定理,存在λ使
 ,再根据向量相等概念解出m即可.
,再根据向量相等概念解出m即可.(3)若
 与
与 垂直,则
垂直,则 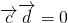 ,化成关于m的方程并解出m即可.
,化成关于m的方程并解出m即可.点评:本题考查向量数量积、夹角的计算,向量共线、向量垂直的条件及判定.是向量中的基本知识,本题属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,
, 和
和 的夹角;
的夹角; 取何值时,
取何值时, 与
与 共线?
共线? ,
,  和
和 的夹角;
的夹角; 取何值时,
取何值时, 与
与 共线?
共线? ,
,  和
和 的夹角;
的夹角; 取何值时,
取何值时, 与
与 共线?
共线? ,
, 和
和 的夹角;
的夹角; 与
与 共线?
共线? 与
与 垂直?
垂直?